Mesopotamische Mathematik: Ein Überblick
Willkommen zur Vorlesung über mesopotamische Mathematik. In dieser Vorlesung werden wir uns intensiv mit der Zahlendarstellung, der historischen Entwicklung Mesopotamiens und ausgewählten algebraischen Aufgaben beschäftigen. Ziel ist es, Ihnen einen ersten Einblick in die mathematischen Praktiken und Errungenschaften dieser alten Zivilisation zu geben.
Schreiben und Rechnen in Mesopotamien
Die Mesopotamier nutzten Tontafeln und Griffel, um ihre Schrift und Berechnungen festzuhalten. Zu Beginn der Schriftentwicklung wurden Zählsteine verwendet, um Mengen zu repräsentieren. Diese Methode war über Jahrtausende im Gebrauch, bis sich schließlich die Keilschrift entwickelte.
Die Keilschrift, die durch das Eindrücken von keilförmigen Zeichen in weichen Ton entstand, entwickelte sich von einfachen Piktogrammen zu abstrakten Symbolen. Es wird vermutet, dass diese schnelle Entwicklung der Schrift auf die Arbeit einer einzelnen Person oder einer kleinen Gruppe zurückzuführen ist.
Die frühesten Schriftzeugnisse sind Wirtschaftstexte aus dem 31. Jahrhundert v. Chr., die Zahlen und verschiedene Arten von Wirtschaftsgütern dokumentieren.
In Mesopotamien gab es den wichtigen Beruf des Schreibers. Sowohl Männer als auch Frauen konnten Schreiber sein und wissenschaftliche Texte verfassen. Die Schreiber trugen die Verantwortung für den Inhalt der Tontafeln.
Ein großer Vorteil der Verwendung von Tontafeln ist ihre Haltbarkeit. Insbesondere wenn die Tafeln gebrannt wurden, blieben sie über Jahrtausende erhalten. Dies ist für Historiker von großem Wert, da viele Tontafeln durch Stadtbrände unbeabsichtigt gebrannt wurden und so erhalten blieben. Ein Beispiel hierfür ist die Bibliothek von Mari, wo eine große Bibliothek durch die Eroberung der Stadt durch Hammurabi erhalten blieb.
Im Vergleich zu Ägypten, aus dem nur wenige mathematische Papyri erhalten sind (wie der Rhind-Papyrus und der Moskauer Papyrus), gibt es aus Mesopotamien Tausende von Tontafeln mit mathematischen Inhalten. Die Erforschung dieser Tafeln ist ein fortlaufender Prozess, der ständig neue Erkenntnisse liefert.
Geometrie in der frühen Zeit
In der frühen mesopotamischen Mathematik wurde die Fläche eines Vierecks oft durch eine Näherung berechnet. Anstatt die exakte Fläche zu berechnen, nutzte man das arithmetische Mittel der gegenüberliegenden Seiten und multiplizierte diese Werte. Diese Methode war sehr praxisorientiert.
Zahlendarstellung
Die Mesopotamier verwendeten verschiedene Zahlendarstellungen, die wichtigsten davon sind:
- Zehnersystem: Ähnlich den römischen Zahlen, aber ohne ein eigenes Zeichen für die Fünf. Zahlen wurden durch die Kombination von Zeichen für Eins und Zehn dargestellt. Dies wurde hauptsächlich für das Abzählen von kleineren Mengen verwendet, nicht zum Rechnen.
- Sexagesimalsystem: Ein Stellenwertsystem zur Basis 60, das für Berechnungen verwendet wurde. Damit beschäftigen wir uns jetzt.
Das Sexagesimalsystem
Das Sexagesimalsystem ist ein Stellenwertsystem, bei dem die Position einer Ziffer eine Potenz von 60 repräsentiert. Die Zahlen von 1 bis 59 wurden durch eine Kombination von Zeichen für 1 und 10 dargestellt.
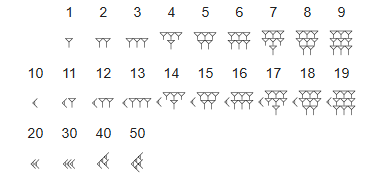
- Beispiele:
- 72 = 𒐕 𒌋𒐖 = 3612
- 2025 = 33 x 60 + 45 = 𒌍𒐗𒐏𒐙
- 20000 = 5 x 60² + 33 x 60 + 20 = 𒐙𒌍𒐗𒑱
- 0,5 = 30 x 60⁻¹ = 𒌍
- 1/3 = 20 x 60⁻¹ = 𒑱
Ein Problem des frühen Sexagesimalsystems war das Fehlen eines Zeichens für die Null. Dies konnte zu Mehrdeutigkeiten bei der Interpretation von Zahlen führen, da die Größenordnung nicht immer klar war. Der Kontext einer Aufgabe half jedoch meistens, die richtige Größenordnung zu bestimmen. Später wurde ein Leerzeichen oder ein Symbol für Null als Platzhalter eingeführt.
Die Wahl der Basis 60 hat mehrere Vorteile, wie z.B. die vielen Teiler der Zahl 60, was das Rechnen mit Brüchen erleichtert. Ein großer Vorteil des Sexagesimalsystems ist, dass viele Brüche als endliche „sexagesimale Brüche“ dargestellt werden können. Dies ist ein Vorteil gegenüber dem Dezimalsystem. Eine mögliche Erklärung für die Verwendung der Basis 60 ist, dass man auf einer Hand bis 12 zählen kann (an den Fingergliedern) und dies mit den fünf Fingern der anderen Hand kombiniert, um auf 60 zu kommen.
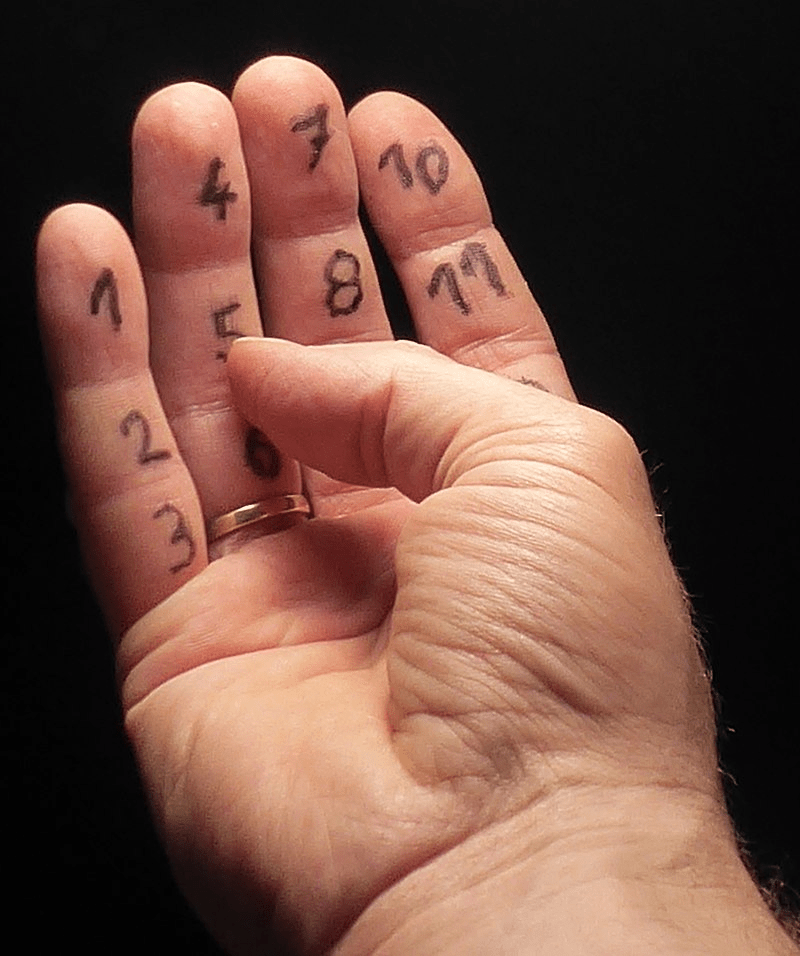
Rechenoperationen
Die Mesopotamier beherrschten die Grundrechenarten. Für die Multiplikation benötigte man das kleine Einmaleins, das im Sexagesimalsystem bis 59 gehen musste. Die Division konnte durch die Multiplikation mit dem Kehrwert durchgeführt werden. Für beide Operationen gab es Tabellen, wo man sowohl das kleine Einmaleins als auch Kehrwerte auslesen konnte.
Die Mesopotamier konnten auch sehr große Zahlen darstellen. Ein Beispiel ist die Zahl 20 hoch 20, deren Darstellung gefunden wurde. Der praktische Nutzen solcher großen Zahlen ist unklar.
Geschichte Mesopotamiens
Mesopotamien, das „Land zwischen den Flüssen“ Euphrat und Tigris, umfasst im Wesentlichen den heutigen Irak und Teile Syriens. Die Landschaft ist überwiegend flach, und die Landwirtschaft ist von Bewässerungssystemen abhängig.
Die Geschichte Mesopotamiens ist reich und vielfältig:
- Frühe Stadtkulturen (ab ca. 9000 v. Chr.): Entstehung erster Städte
- Sumerische Zeit (ab ca. 3100 v. Chr.): Entwicklung der sumerischen Sprache
- Akkadisches Reich (ca. 2350 v. Chr.): Erstes Großreich
- Altbabylonische Zeit (ca. 1800 v. Chr.): Blütezeit unter Hammurabi
- Spätere Reiche: Mittelassyrisches Reich, Reich der Kassiten, Mittelassyrisches Reich, Reich der Hethiter, 2. Dynastie von Isin (Aramäer), Neuassyrisches Reich, Spätbabylonisches Reich (Chaldäer)
- Eroberungen: Reich der Achämeniden (Perser), Alexander der Große/Seleukiden (Makedonen/Griechen)
Die Schrift entwickelte sich von einer reinen Wortschrift zu einer Silbenschrift. In der neuassyrischen Zeit wurden die Zeichen für Zehner und Einer auch für die Silbenschrift verwendet. Ursprünglich standen die Zeichen für ganze Wörter, später für ähnlich klingende Silben. Dies ermöglichte es, mit etwa 300 Zeichen zu schreiben.
Die Entzifferung der Keilschrift ist dadurch erschwert, dass im Laufe der Zeit ähnliche Zeichen für unterschiedliche Wörter oder Laute verwendet wurden.
Bedeutende Herrscher waren z.B. Gilgamesch und Hammurabi.
Mathematische Texte
Die mathematischen Texte aus Mesopotamien, die wir hier behandeln, sind meistens Übungsaufgaben für den Unterricht. Sie verwenden eine spezielle Fachsprache, die für uns oft schwer zu interpretieren ist. Algebraische Manipulationen sind oft mit geometrischem Denken verbunden. Der Realitätsbezug der Aufgaben ist oft fragwürdig oder nicht vorhanden.
Beispiele für mathematische Aufgaben (BM13901)
- Aufgabe 1: „Ich habe die Fläche und die Seite erhalten: 0;45. Was ist die Seite?“
Wir präsentieren hier die geometrische Interpretation von Jens Høyrup.
- Lösung: Die „Fläche“ steht für die Fläche eines Quadrats (c²). Die Aufgabe entspricht in eine moderne anachronistische Schreibweise der quadratischen Gleichung c² + c = 0;45. Die Lösung wird durch einen Algorithmus gefunden, der dem Prinzip der quadratischen Ergänzung entspricht.
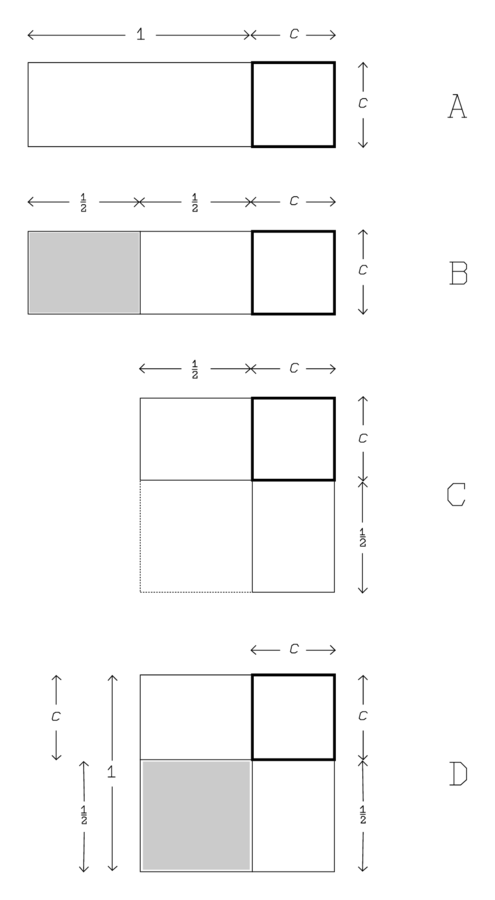
- Der Lösungsweg ist:
Die Gleichung wird durch Ergänzung zu einem Quadrat gelöst
c² wird als Quadrat dargestellt
c wird als Rechteck mit der Breite 1 dargestellt (A)
Brich die 1 in zwei, das ergibt 0;30 (B)
Multipliziere 0;30 mit 0;30 ergibt 0;15
Addiere 0;15 zu 0;45 ergibt 1 (C)
Die Quadratwurzel von 1 ist 1
Subtrahiere 0;30, du hast die Seite 0;30 erhalten (D)
Algebraisch ist die Ideee der Quadratischen Ergänzung, wie wir ihn heute verwenden, das gleiche:
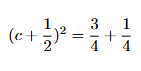
(C) usw.
- Aufgabe 8: „Ich habe die Fläche meiner zwei Rechtecke zusammengefügt: 2140. Ich habe die Seiten zusammengefügt: 50. Was ist das?“
- Lösung: Die „Fläche“ steht für die Summe der Flächen zweier Quadrate (x² + y²). Die „Seiten“ stehen für die Summe der Seiten der Quadrate (x + y). Die Aufgabe führt auf ein System von zwei Gleichungen:
- x² + y² = 2140
- x + y = 50
- Der Lösungsweg ist:
- Halbiere 50: 50 / 2 = 25
- Quadriere das Ergebnis: 25² = 1025
- Halbiere 2140: 2140 / 2 = 1050
- Subtrahiere 1025 von 1050: 1050 – 1025 = 25
- Die Wurzel von 25 ist 5
- Addiere 5 zu 25: 25 + 5 = 30 (erste Seite)
- Subtrahiere 5 von 25: 25 – 5 = 20 (zweite Seite)
- Dieser Lösungsweg entspricht der Anwendung binomischer Formeln.
Die Mesopotamier kannten Lösungsalgorithmen für verschiedene Arten von Gleichungen. Da sie keine Taschenrechner hatten, waren diese Algorithmen für sie effizienter als das Anwenden von Formeln.
Weitere mathematische Errungenschaften
Die Mesopotamier erstellten Tabellen von Kehrwerten. Die Tontafel Plimpton 322 enthält pythagoräische Zahlentripel. Sie kannten auch das babylonische Verfahren zur Annäherung an Quadratwurzeln, ein numerisches Verfahren. Ein beeindruckendes Beispiel zeigt, wie die Babylonier das Diagonale von einem Quadrat extrem gut approximieren konnten.
Weiter Errungenschaften, wie zum Beispiel Flächen und Volumenberechnungen können wir heute leider nicht besprechen, sie finden aber viele Beispiele in den empfohlenen Sekundärquellen.
Allgemeine Werke zur mesopotamischen Mathematik:
- Otto Neugebauer, „The Exact Sciences in Antiquity“: Ein Klassiker, der einen umfassenden Überblick über die Mathematik und Astronomie im alten Mesopotamien und Ägypten bietet. Neugebauer war ein Pionier in der Entzifferung und Interpretation mesopotamischer mathematischer Texte.
- Jens Høyrup, „Lengths, Widths, Surfaces: A Portrait of Old Babylonian Algebra and Its Kin“: Høyrups Werk ist detailliert und untersucht die algebraischen Methoden der Babylonier, oft mit einem Fokus auf die geometrische Interpretation algebraischer Probleme.
- Eleanor Robson, „Mathematics in Ancient Iraq: A Social History“: Robson bietet eine sozialhistorische Perspektive auf die mesopotamische Mathematik und untersucht, wie Mathematik in der Gesellschaft verwendet und praktiziert wurde.
- „Before Pythagoras: The Culture of Old Babylonian Mathematics“ von Karen Rhea Nemet-Nejat: Dieses Buch bietet eine umfassende Einführung in die altbabylonische Mathematik und ihre kulturellen Kontexte.

Hinterlasse einen Kommentar