András Bátkai's Weblog

Die altägyptische Mathematik entwickelte sich in einer Zivilisation, deren Leben stark vom Nil geprägt war. Die jährlichen Überschwemmungen des Nils machten es notwendig, Felder neu zu vermessen und zu verteilen, was zur Entwicklung mathematischer Methoden führte.

Geschichtlicher Hintergrund

Im Vergleich zu Mesopotamien, wo die Menschen zwischen zwei Flüssen siedelten, konzentrierte sich das Leben in Ägypten auf das Gebiet entlang des Nils. Im gegensatz zu Mesopotamien sind die alten Siedlungsstätten bis heute durchgehend besiedelt, was die archäologische Arbeit sehr schwierig machte.

Die ägyptische Geschichte wird in verschiedene Epochen unterteilt, darunter 

• das alte Reich (bekannt für den Pyramidenbau, ca. 2707-2216 v.Chr.)  
• das mittlere Reich (viele mathematische Texte stammen aus diese Zeit, ca. 2137-1781 v.Chr.)
• das neue Reich (mit berühmten Pharaonen wie Echnaton oder Ramses II, ca. 1550-1070 v.Chr.).

Eine wichtige Besonderheit Ägyptens war die frühe Vereinigung von Ober- und Unterägypten, die das politische und kulturelle Leben des Landes nachhaltig prägte.

Schriftentwicklung

Anders als die Mesopotamier, die auf Tontafeln schrieben, verwendeten die Ägypter Papyrus, ein aus der Papyrusstaude hergestelltes Material. Papyrus war zwar ein reichlich vorhandenes Schreibmaterial, aber nicht so haltbar wie Tontafeln. Daher sind weniger zeitgenössische Schriftquellen aus Ägypten erhalten.

Die Entzifferung der ägyptischen Hieroglyphen gelang erst relativ spät, maßgeblich durch den Fund des Rosetta-Steins, der einen dreisprachigen Text (Hieroglyphen, Demotisch und Griechisch) enthält.

Die ägyptische Schrift entwickelte sich von einer reinen Bilderschrift, in der jedes Symbol ein ganzes Wort darstellte, zu einer gemischten Schrift, in der Konsonanten- und Sinnzeichen hinzugekommen sind, so dass sich die Hieroglyphenschrift aus Lautzeichen (Phonogrammen), Bildzeichen (Ideogrammen) und Deutzeichen (Determinativen) zusammensetzt. Es gab verschiedene Schriftarten: Hieroglyphen für offizielle und verzierte Texte und Hieratisch, die kursive Variante für den täglichen Gebrauch.

Die wichtigsten mathematischen Quellen sind der Papyrus Moskau und der Papyrus Rhind. Das sind mathematische Aufgabensammlungen. Der Anfang von Papyrus Rhind wurde von August Eisenlohr in seinem in 1877 herausgegebenen Buch so übersetzt:

Zahlendarstellung

Die Ägypter verwendeten ein Dezimalsystem, d. h. ein Zahlensystem das 10 als Grundlage hatte. Sie hatten eigene Hieroglyphen für 1, 10, 100, 1000 usw.

Zahlzeichen:

• Strich () für 1
• Rindsgespann () für 10
• Seilschlinge () für 100
• Lotusblüte ( ) für 1000
• Zeigefinger ( ) für 10.000
• Kaulquappe ( ) für 100.000
• Göttin ( ) für 1.000.000

Einige Beispiele, wie man Zahlen geschrieben hat:

305 = 42 = 2025 =

Grundlegende Rechentechniken

Die Ägypter beherrschten die Grundrechenarten.

Multiplikation:

• Die Multiplikation wurde durch wiederholte Verdopplung und Addition durchgeführt.
• Beispiel: 41 x 25

1. Erstelle eine Tabelle mit Zweierpotenzen in der linken Spalte und Vielfachen von 25 in der rechten Spalte:

1	25
2	50
4	100
8	200
16	400
32	800

2. Stelle 41 als Summe von Zweierpotenzen dar: 41 = 32 + 8 + 1
3. Addiere die entsprechenden Vielfachen von 25: 800 + 200 + 25 = 1025
4. Ergebnis: 41 x 25 = 1025

• Die Erklärung, warum diese Methode funktioniert basiert auf der Darstellung von Zahlen im Binärsystem (Dualsystem, Basis 2). Sie ist eine Form der wiederholten Addition.

Division:

• Die Division wurde ähnlich wie die Multiplikation durch Verdopplung durchgeführt, aber in umgekehrter Richtung.
• Beispiel: 117 : 9

1. Erstelle eine Tabelle mit Zweierpotenzen in der linken Spalte und Vielfachen von 9 in der rechten Spalte:

1	9
2	18
4	36
8	72

2. Finde eine Kombination von Vielfachen von 9, die 117 ergibt: 72 + 36 + 9 = 117
3. Addiere die entsprechenden Zweierpotenzen: 8 + 4 + 1 = 13
4. Ergebnis: 117 : 9 = 13

• Wenn die Division nicht aufgeht, erhält man einen Rest.
• Beispiel: 19 : 8

1	8
2	16
1/2	4
1/4	2
1/8	1

2. 19 = 16 + 2 + 1
3. Ergebnis: 19 : 8 = 2 + 1/4 + 1/8

Bruchdarstellungen

Die Ägypter bevorzugten Stammbrüche, d. h. Brüche mit dem Zähler 1. Allgemeine Brüche wurden als Summe von Stammbrüchen dargestellt.

• Beispiele:

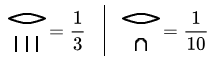
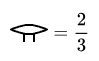
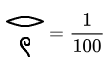
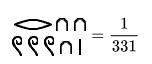
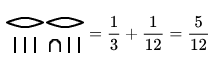
Darstellung von Brüchen:

• Stammbrüche wurden oft durch Hinzufügen eines „Auges“ zu den Zahlzeichen dargestellt.
• Allgemeine Brüche wurden als Zerlegung in Stammbrüche dargestellt.
• Es gab verschiedene Methoden, um allgemeine Brüche in Stammbrüche zu zerlegen. Heute können wir nur Raten, weil es oft kein Recenweg nur Ergebnisse da sind.
• Beispiel: Zerlegung von 2/19

• Mögliche Darstellung: 2/19 = 1/12 + 1/76 + 1/114
• Es gibt verschiedene Algorithmen und Formeln, um solche Zerlegungen zu finden.

Anwendungen der Mathematik

Die ägyptische Mathematik fand Anwendung in verschiedenen Bereichen des täglichen Lebens.

Hau-Rechnungen:

• Dies sind Aufgaben, die linearen Gleichungen ähneln.
• Sie wurden mit einer Methode gelöst, die im Mittelalter als „Regula Falsi“ bekannt war.
• Beispiel: „Ein Haufen und sein Siebtel ergibt 19.“

1. Setze eine beliebige Zahl für den „Haufen“ ein (z.B. 7).
2. Berechne das Ergebnis: 7 + 7/7 = 8
3. Dividiere das tatsächliche Ergebnis (19) durch das berechnete Ergebnis (8): 19/8
4. Multipliziere die angenommene Zahl (7) mit dem Ergebnis: 7 * 19/8 = 16 5/8

Verteilungsprobleme:

• Aufgaben, bei denen es darum ging, Güter (z.B. Brot, Bier) gerecht unter mehreren Personen aufzuteilen.
• Die Lösungen gaben oft nicht nur die Menge an, die jeder Person zusteht, sondern auch eine Anleitung, wie die Güter aufgeteilt werden sollen.
• Beispiel: „Verteile 9 Laib Brot an 10 Männer.“

• Ergebnis: 2/3 + 1/5 + 1/30
• Diese Angabe gibt nicht nur die Menge an Brot pro Mann an, sondern auch, wie das Brot aufgeteilt werden soll.

Viele weitere, hauptsächlich geometrische Themen können wir leider in diesem einen Vortrag nicht behandeln, die findet man aber in der weiterfürenden Literatur.

Literatur:

Neugebauer, O. (1969): Vorlesungen über Geschichte der antiken mathematischen Wissenschaften, Springer-Verlag

Wußing, H., Alten, H., Wesemüller-Kock, H. (2008). 6000 Jahre Mathematik: Eine kulturgeschichtliche Zeitreise – 1. Von den Anfängen bis Leibniz und Newton. Deutschland: Springer Berlin Heidelberg.

Herrmann, D. (2019). Mathematik im Vorderen Orient: Geschichte der Mathematik in Altägypten und Mesopotamien. Deutschland: Springer Berlin Heidelberg.

Gericke, H. (2013). Mathematik in Antike und Orient. Deutschland: Springer Berlin Heidelberg.

Struik, D. J. (2013). Abriss der Geschichte der Mathematik. Deutschland: Vieweg+Teubner Verlag.