András Bátkai's Weblog

Die Vorlesung behandelt Euklids „Elemente“ (Στοιχεῖα Stoicheia), ein Werk, das die Mathematikgeschichte maßgeblich geprägt hat.

Euklid: Die Person

Über die Person Euklid selbst ist wenig bekannt. Es wird angenommen, dass er um 300 v. Chr. in Alexandria, Ägypten, lebte. Er war wahrscheinlich am Museion von Alexandria tätig, einem Zentrum für Wissenschaft und Forschung. Euklid verfasste nicht nur die „Elemente“, sondern auch andere mathematische und astronomische Werke.

Die Elemente: Inhalt und Bedeutung

Die „Elemente“ sind eine systematische Zusammenstellung des mathematischen Wissens der damaligen Zeit, insbesondere der Geometrie und Zahlentheorie. Obwohl auch vor Euklid Bücher mit dem Titel „Elemente“ existierten, erlangte Euklids Werk eine so herausragende Bedeutung, dass die älteren Werke nicht mehr kopiert wurden und verloren gingen.

Die „Elemente“ bestehen aus 13 Büchern, wobei die letzten zwei Bücher wahrscheinlich später hinzugefügt wurden. Die Bücher sind thematisch geordnet:

• Buch 1-4: Grundlegende Geometrie (Punkte, Linien, Flächen, Dreiecke, Vierecke, Kreise)
• Buch 5-6: Proportionen (möglicherweise auf der Arbeit von Eudoxos basierend)
• Buch 7-9: Zahlentheorie
• Buch 10: Inkommensurabilität
• Buch 11-13: Raumgeometrie

Mathematischer Ostrakon von Elephantine

Ein Ostrakon (eine beschriebene Tonscherbe) aus Elephantine, datiert auf ca. 250 v. Chr., enthält einen Text, der sich mit der Konstruktion eines Ikosaeders befasst. Dieser Fund ist von Bedeutung, da er das älteste erhaltene griechische Manuskript ist, das einen Text aus Euklids „Elementen“ enthält.

Aufbau der Elemente

Euklids „Elemente“ sind axiomatisch aufgebaut. Das bedeutet, dass das Werk auf einer Reihe von Definitionen, Axiomen und Postulaten basiert, aus denen dann alle weiteren Sätze (Theoreme) logisch abgeleitet werden.

• Definitionen: Euklid beginnt mit der Definition grundlegender geometrischer Objekte wie Punkt, Linie, Fläche, Winkel usw.. Diese Definitionen entsprechen nicht immer den heutigen mathematischen Definitionen, sondern beschreiben eher die Eigenschaften der Objekte.
• Axiome (Gemeinsame Begriffe): Dies sind allgemeine Regeln der Gleichheit, z. B. „Wenn Gleiches zu Gleichem addiert wird, sind die Summen gleich“.
• Postulate: Dies sind geometrische Konstruktionsanweisungen, z. B. „Es sei gefordert, von jedem Punkt nach jedem Punkt eine Gerade zu ziehen“.

Beweismethoden

Euklids „Elemente“ verwenden verschiedene Beweismethoden, um die mathematischen Aussagen zu begründen. Die wichtigsten sind:

• Demonstrative Beweise (Direkte Beweise): Dies sind die grundlegendsten Beweise, bei denen die Behauptung durch eine Reihe logischer Schlussfolgerungen direkt aus den Definitionen, Axiomen und bereits bewiesenen Sätzen abgeleitet wird.
  
  • Beispiel: Euklid beweist, dass die Summe zweier gerader Zahlen gerade ist. Er definiert gerade Zahlen als Zahlen, die in zwei gleiche Teile geteilt werden können. Dann zeigt er, dass, wenn man zwei solche Zahlen addiert, die resultierende Zahl ebenfalls in zwei gleiche Teile geteilt werden kann, und somit gerade ist. In modernen Begriffen würde man sagen: Seien 2a und 2b zwei gerade Zahlen, wobei a und b ganze Zahlen sind. Ihre Summe ist 2a + 2b = 2(a+b). Da a+b eine ganze Zahl ist, ist 2(a+b) definitionsgemäß gerade.
• Reductio ad absurdum (Indirekter Beweis): Bei dieser Methode wird angenommen, dass die zu beweisende Behauptung falsch ist. Anschließend wird gezeigt, dass diese Annahme zu einem Widerspruch führt, d. h., dass aus der Annahme eine Aussage folgt, die offensichtlich falsch ist oder den Axiomen und Postulaten widerspricht. Da ein Widerspruch nicht wahr sein kann, muss die ursprüngliche Annahme falsch sein, und somit ist die zu beweisende Behauptung wahr.
  
  • Beispiel: Euklids Beweis für die Unendlichkeit der Primzahlen. Genauer gesagt (Euklid hat die Unendlichkeit vermieden), für eine beliebige endliche Menge von Primzahlen gibt es immer eine Primzahl, die da nicht enthalten ist.
    1. Annahme: Es gibt nur endlich viele Primzahlen: p1, p2, …, pn.
    2. Konstruiere die Zahl N = (p1 * p2 * … * pn) + 1 (also das Produkt aller Primzahlen plus 1).
    3. Fall 1: N ist prim. Dann ist N eine Primzahl, die nicht in der ursprünglichen Liste enthalten ist, was der Annahme widerspricht.
    4. Fall 2: N ist nicht prim. Dann muss N durch eine Primzahl teilbar sein (Dies wurde vorhin bewiesen). Keine der Primzahlen p1, p2, …, pn teilt N, da bei der Division immer der Rest 1 bleibt. Also muss es eine andere Primzahl geben, die N teilt, was wieder der Annahme widerspricht.
    5. Schlussfolgerung: In beiden Fällen führt die Annahme zu einem Widerspruch, also muss es unendlich viele Primzahlen geben. 
• Konstruktionsbeweise: Hier wird die Existenz eines mathematischen Objekts (z. B., einer Linie, eines Dreiecks) bewiesen, indem es mit den in den Postulaten erlaubten Konstruktionsschritten (Zirkel und Lineal) konstruiert wird.
  
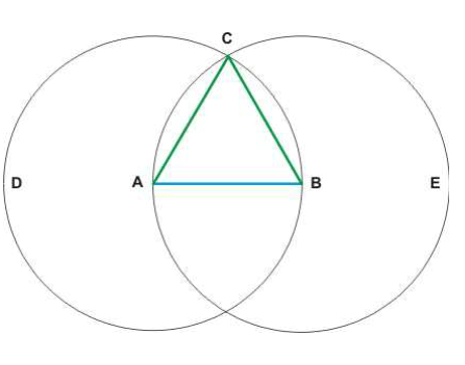
  • Beispiel: Euklids Konstruktion eines gleichseitigen Dreiecks über einer gegebenen Strecke AB.
    1. Zeichne einen Kreis mit Mittelpunkt A und Radius AB.
    2. Zeichne einen Kreis mit Mittelpunkt B und Radius BA (was dem Radius AB entspricht).
    3. Sei C der Schnittpunkt der beiden Kreise.
    4. Zeichne die Strecken AC und BC.
    5. Beweis: Da AC und AB Radien des ersten Kreises sind, gilt AC = AB. Da BC und AB Radien des zweiten Kreises sind, gilt BC = AB. Aus der Transitivität der Gleichheit folgt AC = BC. Somit hat das Dreieck ABC drei gleich lange Seiten und ist gleichseitig.

Ein anderer Konstruktionsbeweis ist der Satz über die Winkelsumme der Dreieck (I.32):

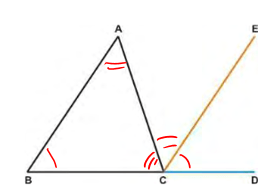
Man konstruiere die Gerade CE, die parallel zu AB ist. Dann sieht man die Gleichheit der entsprechenden Winkel und dass sie zusammen zwei rechten Winkel ergeben.

Wichtige Resultate in den Elementen

Die „Elemente“ enthalten zahlreiche bedeutende mathematische Resultate, darunter:

• Das Parallelenaxiom
• Der Satz des Pythagoras
• Der Satz über die Winkelsumme im Dreieck
• Der Euklidische Algorithmus zur Bestimmung des größten gemeinsamen Teilers
• Der Beweis für die Existenz unendlich vieler Primzahlen
• Der Beweis für die Irrationalität der Quadratwurzel von 2

Euklids Elemente und seine Wirkung

Die „Elemente“ hatten einen enormen Einfluss auf die Entwicklung der Mathematik und dienten lange Zeit als Standardlehrbuch für Geometrie.

Die Axiomatische Methode

Die „Elemente“ sind ein frühes Beispiel für die axiomatische Methode, bei der eine Theorie auf einer Reihe von Grundannahmen (Axiomen) aufgebaut wird.

• Axiomensystem: Ein Axiomensystem besteht aus einer Sprache und einer Menge von Axiomen.
• Axiome: Axiome sind Grundannahmen, die innerhalb des Systems nicht bewiesen werden.
• Theoreme: Theoreme sind Aussagen, die logisch aus den Axiomen abgeleitet werden.

Axiomatische Methode: Beispiele

Die axiomatische Methode ist ein grundlegendes Prinzip in der Mathematik, bei dem eine Theorie auf einer Reihe von Grundannahmen (Axiomen) aufgebaut wird. Dieses Prinzip findet jedoch nicht nur in der Mathematik Anwendung, sondern auch in anderen Disziplinen.

1. Mathematik

In der Mathematik ist die axiomatische Methode allgegenwärtig. Ein klassisches Beispiel ist die axiomatische Definition einer Gruppe.

• Gruppentheorie: Eine Gruppe ist eine Menge G zusammen mit einer Verknüpfung (oft als Multiplikation notiert), die folgende Axiome erfüllt:
  
  • Assoziativität: (a * b) * c = a * (b * c) für alle a, b, c in G.
  • Neutrales Element: Es gibt ein Element e in G, so dass e * a = a * e = a für alle a in G.
  • Inverses Element: Für jedes a in G gibt es ein Element a⁻¹ in G, so dass a * a⁻¹ = a⁻¹ * a = e.
• Aus diesen wenigen Axiomen lässt sich eine Vielzahl von Sätzen über Gruppen ableiten, unabhängig davon, was die Elemente der Gruppe konkret sind (Zahlen, Funktionen, Symmetrieoperationen usw.).  

2. Ethik

Auch in der Philosophie gab es Versuche, ethische Theorien axiomatisch aufzubauen.

• Spinozas Ethik: Der Philosoph Baruch Spinoza (1632-1677) versuchte in seinem Werk „Ethik“ (1677) ein System der Ethik zu entwickeln, das auf Definitionen und Axiomen basiert, ähnlich wie Euklids Geometrie.
  
  • Spinoza beginnt mit Definitionen von Begriffen wie „Ursache“, „Substanz“, „gut“ und „böse“.  
  • Dann formuliert er Axiome über die Natur des Menschen und der Realität.
  • Aus diesen Definitionen und Axiomen leitet er dann Lehrsätze über menschliche Emotionen, Handlungen und Tugenden ab.  
  • Zum Beispiel argumentiert Spinoza, dass der Mensch, der von der Vernunft geleitet wird, in einem Staat, in dem er nach gemeinschaftlichem Beschluss lebt, freier ist als in der Einsamkeit.  
• Obwohl Spinozas Ansatz nicht im heutigen Sinne mathematisch formal ist, zeigt er den Versuch, ethische Überzeugungen auf eine systematische, deduktive Grundlage zu stellen.  

3. Physik

Die Physik verwendet ebenfalls axiomatische Strukturen, insbesondere in der theoretischen Physik.

• Newtonsche Mechanik: Isaac Newtons (1643-1727) Bewegungsgesetze sind ein klassisches Beispiel für Axiome in der Physik.
  3. Gesetz (Trägheitsgesetz): Ein Körper verharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, sofern er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern.
  4. Gesetz (Grundgesetz der Mechanik): Die Änderung der Bewegung ist der einwirkenden bewegenden Kraft proportional und erfolgt in der Richtung derjenigen geraden Linie, in welcher diese Kraft wirkt.
  5. Gesetz (Wechselwirkungsgesetz): Kräfte treten immer paarweise auf. Übt ein Körper A auf einen anderen Körper B eine Kraft aus (actio), so übt auch Körper B auf Körper A eine gleich große, entgegengesetzt gerichtete Kraft aus (reactio).
• Diese Gesetze sind Grundannahmen, die nicht bewiesen werden, sondern auf Beobachtung und Experiment beruhen. Aus ihnen lassen sich zahlreiche andere physikalische Gesetze und Phänomene ableiten.  

4. Kommunikationswissenschaft

Auch in den Sozialwissenschaften gibt es Ansätze, Theorien axiomatisch zu formulieren.

• Watzlawicks Kommunikationsaxiome: Der Kommunikationswissenschaftler Paul Watzlawick (1921-2007) entwickelte eine Theorie der menschlichen Kommunikation, die auf einigen grundlegenden Axiomen basiert.
  • Ein bekanntes Axiom ist: „Man kann nicht nicht kommunizieren.“  
  • Dieses Axiom besagt, dass jedes Verhalten in einer sozialen Situation als Kommunikation aufgefasst wird, auch wenn es nicht beabsichtigt ist.
  • Weitere Axiome betreffen den Inhalts- und Beziehungsaspekt von Kommunikation, die Interpunktion von Ereignisfolgen, digitale und analoge Modalitäten sowie symmetrische und komplementäre Beziehungen.  
• Diese Axiome dienen als Grundlage für das Verständnis von Kommunikationsprozessen und -störungen.  

5. Wirtschaftswissenschaft

In der Wirtschaftswissenschaft, insbesondere in der neoklassischen Theorie, werden Modelle auf axiomatischen Annahmen über das Verhalten von Wirtschaftsakteuren aufgebaut.  

• Axiome des rationalen Handelns: Ein zentrales Axiom ist das der Rationalität, das besagt, dass Individuen danach streben, ihren Nutzen zu maximieren.
  
• Weitere Axiome betreffen Präferenzen (Vollständigkeit, Transitivität), Informationen und Märkte.
  
  Auf Basis dieser Axiome werden Modelle entwickelt, um wirtschaftliche Phänomene zu erklären und vorherzusagen.  

Diese Beispiele zeigen, dass die axiomatische Methode ein vielseitiges Werkzeug ist, das in verschiedenen Disziplinen eingesetzt wird, um Theorien zu strukturieren, logische Schlussfolgerungen zu ziehen und unser Verständnis der Welt zu verbessern. Das alles zeig den Enormen Einfluss dieses Werks auf unsere Kultur.

Literatur:

http://www.opera-platonis.de/euklid/Euklid_Stoicheia.pdf

Wardhaugh, B. (2022). Begegnungen mit Euklid–Wie die» Elemente «die Welt veränderten. HarperCollins.

Schönbeck, J. (2013). Euklid: um 300 v. Chr (Vol. 12). Springer-Verlag.

Schreiber, P. (2013). Euklid (Vol. 87). Springer-Verlag.

Byrne, O. (1847). The first six books of the Elements of Euclid: in which coloured diagrams and symbols are used instead of letters for the greater ease of learners. William Pickering. Online: https://www.c82.net/euclid/#books

https://www.ams.org/publicoutreach/feature-column/fc-2011-11