András Bátkai's Weblog

Einleitung

Heute begeben wir uns auf eine Reise in eine Epoche, die auf den ersten Blick vielleicht nicht als Hochburg der Mathematik erscheint: die Zeit der Reformation. Doch hinter den religiösen und gesellschaftlichen Umwälzungen dieser Zeit verbirgt sich auch eine spannende Geschichte mathematischer Entdeckungen und Leistungen. Wir werden uns heute mit drei Mathematikern beschäftigen, deren Wirken in diese Zeit fällt und deren Beiträge die Entwicklung der Mathematik nachhaltig beeinflusst haben: Michael Stifel, Georg Joachim Rheticus und Jost Bürgi. Wir konzentrieren hier auf ihr mathematische Leistung, man sollte aber nicht vergessen dass sie in anderen bereichen auch großartiges geleistet haben.

Die Universität Wittenberg und die Mathematik

Es ist wichtig zu betonen, dass die Universität Wittenberg, an der auch die Mathematiker Stifel und Rheticus wirkten, eine wichtige Rolle in der Förderung von Mathematik und Wissenschaft während der Reformation spielte. Die Universität wurde 1502 gegründet und entwickelte sich zu einem Zentrum der Gelehrsamkeit, auch dank der Unterstützung von Reformatoren wie Martin Luther und Philipp Melanchthon. 1514 wurde Mathematik offiziell als eigenständiges Lehrfach an der Universität eingeführt, was ihre wachsende Bedeutung unterstrich. In 1521 forderten Luther und Melanchton zwei eigenständige Mathematiklehrstühle. 

Michael Stifel (1487 – 1567)

Beginnen wir mit Michael Stifel. Geboren in Esslingen, Deutschland, war Stifel eine faszinierende Persönlichkeit, die auf den ersten Blick vielleicht nicht den typischen Mathematiker verkörperte. Stifel war zunächst Augustinerermönch und später Pfarrer. Seine Leidenschaft für Zahlen entwickelte sich aus seinem intensiven Studium der Bibel. Er war fasziniert von den Mustern und vermeintlichen verborgenen Bedeutungen, die er in Zahlen zu entdecken glaubte.

Stifel leitete dieses Datum aus einer numerologischen Analyse des Satzes „Videbunt in quem transfixerunt“ (Sie werden sehen, wen sie durchbohrt haben) aus dem Johannesevangelium ab. Seine Berechnungen des Jahres 1533 basierten auf der Umordnung der römischen Ziffern MDXVVVVIII in diesem Satz. Den Rest des Datums hat er durch die mystische Bedeutung des Zahles 42=6*7  berechnet, somit hat er den 42. Sonntag, 19. Oktober bekommen.

Stifels Prophezeiung hatte reale Auswirkungen. Seine Gemeinde bereitete sich auf das nahende Ende vor, stellte ihre Arbeit ein und verschenkte ihren Besitz. Das Ausbleiben des Weltuntergangs führte zu Stifels Verhaftung.

„Arithmetica Integra“ und der Exponent: Doch Stifels Beitrag zur Mathematik geht weit über seine eschatologischen Berechnungen hinaus. Sein Hauptwerk, die „Arithmetica Integra“ (1544), ist ein bedeutendes Werk der frühen Neuzeit.

In diesem Buch führte Stifel den Begriff „Exponent“ ein, der heute aus der Mathematik nicht mehr wegzudenken ist. Er stellte Rechenregeln für Potenzen mit gleicher Basis vor und erkannte den Zusammenhang zwischen arithmetischen und geometrischen Reihen.

Stifel erkannte, dass Multiplikations- und Divisionsoperationen in einer geometrischen Reihe durch Additions- und Subtraktionsoperationen in der entsprechenden arithmetischen Reihe abgebildet werden können.

Beispiel: Die Tabelle ordnet Exponenten zur Basis 2 den entsprechenden Potenzwerten zu:

…	-3	-2	-1	0	1	2	3	4	…
…	1/8	1/4	1/2	1	2	4	8	16	…

Stifel gab explizit Beispiele für das Rechnen mit negativen Exponenten.

Für uns zur Veranschaulichung: Der Produkt 8*¼ entspricht bei den Exponenten 3+(-2)=1, somit ist das Ergebnis 8*¼ = 2.

Irrationale Zahlen und Wurzelberechnung: Stifel beschäftigte sich auch mit irrationalen Zahlen, die er als „Größe“ oder „numeri absurdi“ (absurde Zahlen) bezeichnete, und entwickelte Methoden zur Berechnung von Wurzeln höherer Ordnung.

Er beschrieb eine Methode zur Wurzelberechnung unter Verwendung von Binomialkoeffizienten.

Lösung quadratischer Gleichungen: Ein weiterer wichtiger Beitrag Stifels ist seine Normalform zur Lösung quadratischer Gleichungen, die es ermöglichte, verschiedene Lösungstypen zusammenzufassen.

Er nannte seine Methode „AMASIAS“, wobei jeder Buchstabe einen Arbeitsschritt repräsentierte.

Georg Joachim Rheticus (1514 – 1574)

Nun wenden wir uns Georg Joachim Rheticus zu, einem Mathematiker und Astronomen, der vor allem für seine Rolle bei der Verbreitung des kopernikanischen Weltbilds bekannt ist. 

Rheticus wurde als Georg Joachim Iserin in Feldkirch, (heute in Vorarlberg, Österreich), geboren. Er der Sohn von Georg Iserin (um 1480–1528), dem Stadtarzt von Feldkirch, und der norditalienischen Adligen Thomasina de Porris (um 1495–1554). Sein Vater wurde 1528 wegen angeblicher Hexerei und Betruges angeklagt und hingerichtet. Nach der Hinrichtung seines Vaters nannte er sich nach dem Familiennamen seiner Mutter Georg Joachim de Porris.

Georg Joachim lernte zunächst an der Lateinschule in Feldkirch und studierte von 1528 bis 1531 in Zürich Mathematik, danach an der Universität Wittenberg, wo er sich 1536 den akademischen Grad eines Magister artium (M.A.) erwarb. Nach einer Studienreise in Nürnberg, Ingolstadt, Tübingen und Feldkirch, weilte Rheticus  1539 bis 1541 bei Kopernikus in Frauenburg.

Rheticus‘ Begegnung mit Nikolaus Kopernikus war ein Wendepunkt in seinem Leben.  Er wurde zu einem leidenschaftlichen Verfechter des heliozentrischen Weltbilds und verfasste die „Narratio Prima“ (1540), eine frühe Darstellung der kopernikanischen Theorie. Die „Narratio Prima“ gilt als die erste veröffentlichte Abhandlung, die Kopernikus‘ revolutionäre Ideen einem breiteren Publikum zugänglich machte.

Trigonometrische Tabellen: Rheticus‘ bedeutendster mathematischer Beitrag sind seine umfangreichen trigonometrischen Tabellen. Er erkannte die Bedeutung genauer trigonometrischer Daten für die Astronomie und widmete einen Großteil seiner Karriere der Erstellung solcher Tabellen.

Sein Hauptwerk, der „Opus Palatinum de triangulis“ (vollendet 1596 von seinem Schüler Valentinus Otho), war ein monumentales Tabellenwerk, das die Werte aller sechs trigonometrischen Funktionen für jeden Bogen in Schritten von 10 Bogensekunden berechnete. Dieses Werk umfasste über 1500 Seiten und war das Ergebnis jahrelanger intensiver Arbeit.

Rheticus führte neue Methoden und Techniken zur Berechnung trigonometrischer Funktionen ein und verbesserte die Genauigkeit erheblich.

Seine Tabellen waren für Jahrhunderte die genauesten ihrer Art und revolutionierten die astronomische Berechnung.

Jost Bürgi (1552 – 1632)

Der dritte Mathematiker, den wir heute betrachten, ist Jost Bürgi, ein Schweizer Uhrmacher und Instrumentenbauer, der sich unabhängig von John Napier mit der Entwicklung von Logarithmen beschäftigte.

Uhrmacher und Instrumentenbauer: Bürgi war ein hochqualifizierter Handwerker, der für seine präzisen Uhren und astronomischen Instrumente bekannt war.

Seine Globen und astronomischen Instrumente waren technologische Meisterwerke seiner Zeit.

Logarithmen: Unabhängig von Napier entwickelte Bürgi eine Methode zur Vereinfachung von Berechnungen, die auf Logarithmen basierte. Seine Logarithmentabellen, die „Arithmetische und geometrische Progreßtabulen“ (1620), erschienen jedoch erst nach Napiers „Mirifici Logarithmorum Canonis“ (1614).

Obwohl Napiers Tabellen früher veröffentlicht wurden, gilt Bürgis Arbeit als unabhängig und möglicherweise früher entwickelt. Bürgis Tabellen hatten einige Vorteile gegenüber Napiers, insbesondere hinsichtlich ihrer Genauigkeit und Benutzerfreundlichkeit.

Bürgis „rote und schwarze Zahlen“: Bürgi entwickelte ein eigenes System zur Veranschaulichung und Berechnung von Logarithmen, das er mit „roten“ und „schwarzen Zahlen“ darstellte.

Bürgis Methode basierte auf der Beobachtung Stiefels, dass bei einer geometrischen Reihe (z.B., 1, 10, 100, 1000…) die Multiplikation von Zahlen durch Addition der entsprechenden Exponenten (in diesem Fall die Anzahl der Nullen: 0, 1, 2, 3…) ersetzt werden kann.

Um dies zu veranschaulichen, schrieb Bürgi die Zahlen einer geometrischen Reihe „schwarz“ und die entsprechenden Exponenten „rot“.

Er hat auch festgestellt, dass es reicht, eine Tabelle nur für die Zahlen zwischen 1 bis 10 zu erstellen, weil jede andere Zahl durch Skalieren somit erreichbar ist.

Der wichtigste Beitrag Bürgis war die richtige Wahl dieser roten und schwarzen Zahlen. Er suchte sich eine Basis, die die weitere Berechnung der Exponenten einfacher gestaltet. Schauen wir uns dazu einen Beispiel an. 

Falls 1,000120000=7,388, dann ist 1,000120001=7,388*0,0001 = 7,388317+0,0007388317 =7,389056…

Somit kann man den nächsten Exponenten sehr schnell berechnen. Durch die Wahl der Nullen kann man die Genauigkeit der Berechnung steuern.

Um nun einen Produkt zu berechnen, addiert man die entsprechenden roten Zahlen und findet in der Tabelle, was die schwarze Zahl zum roten ist.

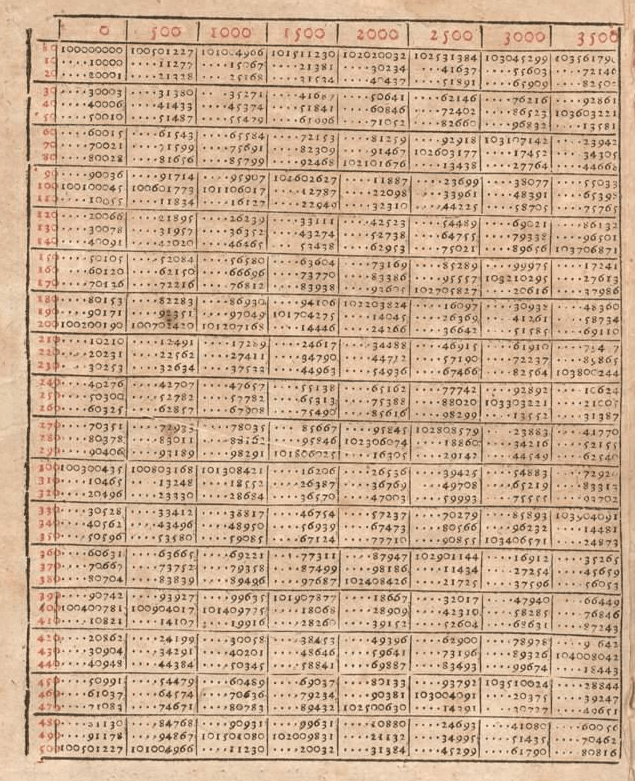
Bürgi erweiterte dieses System auch für nicht ganzzahlige Exponenten, was seiner Methode eine breitere Anwendbarkeit verlieh.

Die Bedeutung der Logarithmen: Die Logarithmen von Napier und Bürgi revolutionierten die numerische Berechnung, insbesondere in der Astronomie und Navigation. Sie ermöglichten es, Multiplikationen und Divisionen durch einfacheres Addieren und Subtrahieren von Logarithmen zu ersetzen. Kepler bedankt sich explizit bei Bürgi für die Möglichkeit, präzisere Berechnungen machen zu können.

Fazit

Die Mathematiker der Reformation trugen auf vielfältige Weise zur Entwicklung der Mathematik bei. Ihre Arbeit reichte von der Zahlentheorie und Algebra bis zur Trigonometrie und der Entwicklung von Rechenhilfsmitteln wie den Logarithmen. Sie zeigten, dass auch in einer Zeit der tiefgreifenden religiösen und gesellschaftlichen Veränderungen die Mathematik einen wichtigen Platz in der intellektuellen Landschaft einnahm.

Vortrag an der PH Vorarlberg im WS24/25 für Lehramtsstudierende des Fachs Matheamtik im Verbund West.