András Bátkai's Weblog

Herzlich willkommen zu dieser vertiefenden Vorlesung über die Schnittstellen von Mathematik und Ästhetik. Wir werden uns heute mit der Rolle der Mathematik in der Schönheit sowie der inhärenten Schönheit der Mathematik selbst auseinandersetzen.

I. Mathematik in der Schönheit

Die Frage nach der Schönheit ist ein fundamentales und altes Thema der Philosophie, das seit der Antike neben Fragen der Gerechtigkeit oder des Sinnes des Lebens diskutiert wird. Obwohl die Schönheit ein zentrales philosophisches Konzept darstellt, ist ihre Bedeutung in der modernen Mainstream-Philosophie, insbesondere im 20. Jahrhundert, zugunsten sprachphilosophischer Ansätze in den Hintergrund getreten. Dennoch lässt sich die tiefgreifende Verbindung zwischen Mathematik und Ästhetik in vielfältigen historischen und kulturellen Kontexten nachweisen.

Ich möchte hier diese Verbindung in einer subjektiven Auswahl aufzeigen. Die Möglichkeiten, weitere Verbindungen zu finden, sind unendlich. Denken wir zum Beispiel an die erste Vorlesung, wo die Bedeutung von geometrischer Kunst in frühen Kulturen diskutiert wurde.  

A. Musik und die Pythagoräer

Die Pythagoräer, eine einflussreiche philosophische und religiöse Bruderschaft, gegründet von Pythagoras von Samos (ca. 570–490 v. Chr.), befassten sich intensiv mit Musik und Musiktheorie. Für sie war Musik eine der vier Grundwissenschaften, die als Teil der Mathematik verstanden wurde. Im Gegensatz zur populären Musik, die man einfach hören und genießen kann, erfordert die Schaffung, Interpretation und theoretische Auseinandersetzung mit Musik ein tiefes Verständnis und erlernte Fähigkeiten.

Die Einteilung der Mathematik bei den Pythagoräern sah folgendermaßen aus:

• Arithmetik (statische Zahlenlehre)
• Musik (dynamische Zahlenlehre)
• Geometrie (statische Raumlehre)
• Astronomie (dynamische Geometrie)

Diese Klassifikation basierte auf der Vorstellung, dass Planeten als Götter galten und ihre Bewegungen (Astronomie) als Ausdruck einer göttlichen Ordnung durch Zahlen zu erforschen waren. Die Musik, ebenfalls göttlichen Ursprungs, offenbarte sich in präzisen Zahlenverhältnissen, die bis heute die Grundlage der Musiktheorie bilden, wie z.B. die Oktave, Quinte, Quarte. Die lateinische Fachsprache der Musiktheorie, die in Europa Verbreitung fand, wurde maßgeblich durch Cicero geprägt, der griechische wissenschaftliche und mathematische Begriffe ins Lateinische übersetzte. Die Verwendung von Begriffen wie Oktave und Quinte in der Musik ist somit ein direktes Erbe der pythagoräischen Harmonielehre.

Ein zentrales Konzept der Pythagoräer war die Sphärenharmonie (lateinisch: Harmonia Mundi oder Musica Universalis). Diese besagt, dass die Himmelskörper – die fünf damals bekannten Planeten sowie Sonne und Mond – auf verschiedenen Sphären kreisen. Die Bewegung dieser Sphären erzeugt durch Reibung eine göttliche Musik, die Pythagoras angeblich hören konnte. Die menschliche Unfähigkeit, diese Musik wahrzunehmen, wurde damit erklärt, dass ein ständig präsentes Geräusch vom Gehirn ausgeblendet wird. Die Idee der Sphärenharmonie fand auch Eingang in die islamische christliche Theologie, beispielsweise im Konzept der „sieben Himmel“.

Anicius Manlius Severinus Boethius (ca. 480–524 n. Chr.), ein römischer Philosoph und Staatsmann, spielte eine entscheidende Rolle bei der Übertragung antiken griechischen Denkens ins lateinische Mittelalter. In seinem Werk De institutione musica (Lehrbuch der Musik) und in De consolatione philosophiae (Trost der Philosophie), das er während seiner Gefangenschaft verfasste, befasste er sich intensiv mit der Musiktheorie. Er unterschied drei Arten von Musik:

1. Musica mundana (Weltenmusik): Die Harmonie, die sich im Kosmos, den Elementen und dem Wechsel der Jahreszeiten offenbart.
2. Musica humana (menschliche Musik): Die Harmonie im Menschen selbst, die den Körper und die Seele verbindet.
3. Musica instrumentalis (Instrumentalmusik): Die Musik, die auf Instrumenten wie der Kithara oder Flöten gespielt wird.

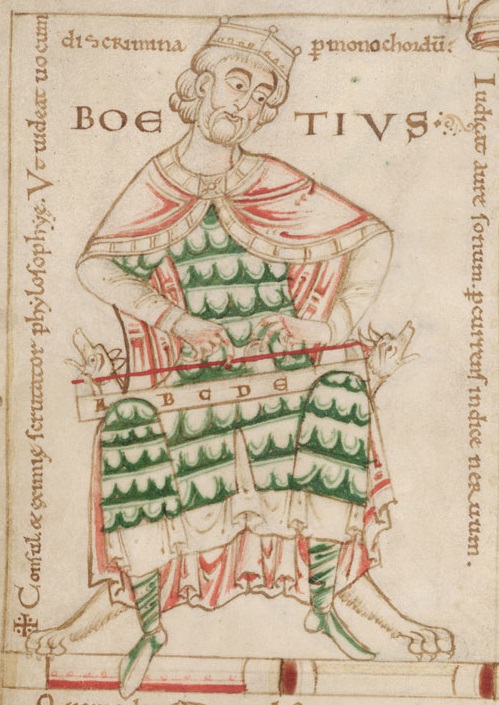
Die Idee der Sphärenmusik wurde auch in der Literatur regelmäßig aufgegriffen.  Goethe zum Beispiel griff die Idee der Weltenmusik später in seinem Faust auf, indem er die Sonne besang, die „nach alter Weise / in Brudersphären Wettgesang“ tönt.

Die Pythagoräer erkannten auch, dass die direkte Aneinanderreihung von musikalischen Intervallen wie Oktaven mathematisch nicht perfekt aufgeht und eine Korrektur erforderlich ist. Dies führte zur Entwicklung von Lösungen für das musikalische Dilemma des pythagoreischen Kommas.

Schwingen zwei Töne im Verhältnis 2:3, so nennt man den Tonsprung eine reine Quint (zum Beispiel von C nach G, was 7 Halbtonschritten entspricht, 7 Tasten weiter auf dem Klavier). Das Zusammenklingen der beiden Töne empfinden wir als besonders schön und angenehm, weil das besonders einfache Verhältnis 2:3 im Ohr quasi „schnell aufgeht“ und weil es überhaupt in jedem auf einem Instrument angespielten Ton als Verhältnis des 1. zum 2. Oberton in natürlicher Weise ohne unser Zutun mitschwingt. Der erste Oberton eines angespielten Grundtones schwingt nämlich doppelt so schnell wie dieser (Oktave), der zweite Oberton drei Mal so schnell wie der Grundton. Also ist das Schwingungsverhältnis zwischen 1. und 2. Oberton 2:3, sprich eine reine Quint. Die einfachsten Schwingungsverhältnisse 1:2 (Oktave) und 1:3 (reine Quint der Oktave) der Obertonreihe empfinden wir daher als besonders schön.
Die reine Quint eines Grundtons schwingt somit mal so schnell wie dieser. Weil die Siebnerreihe erst nach 12 Schritten wieder auf die Zwölferreihe trifft, , müssten also 12 reine Quintensprünge idealerweise exakt auf 7 Oktavensprünge führen. Das können sie aber unmöglich, weil nicht gleich sein kann (die erste Zahl hat den Nenner , die zweite ist natürlich).

Die temperierte Stimmung besteht darin, dass man für jeden Halbtonsprung aufwärts den Faktor verwendet. Nach zwölf temperieten Halbtönen erreicht man damit den Schwingungsverhältnis-Faktor 2, also eine Oktave. Eine temperierte Quint, das heißt ein Sprung von 7 temperierten Halbtönen, entspricht somit . Eine reine Quint hingegen entspricht dem Faktor 3/2 = 1,5, das heißt sie ist ganz leicht höher als die temperierte Quint. Die temperierte Quint hoch 12 ergibt exakt 7 Oktaven, nämlich . Dagegen ergibt die 12. Potenz der reinen Quint den Faktor , also einen merklichen Unterschied zur 7. Oktave. Diesen faktoriellen Unterschied nennt man eben das pythagoreische Komma.
Die Stimmung eines Klaviers ist temperiert. Wie oben gesehen, stimmt eine temperierte Quint, zum Beispiel von C nach G aufwärts, auf dem Klavier eh ziemlich gut überein mit einer reinen Quint. Bei anderen Tonsprüngen unterscheiden sich die temperierte und die reine „Fassung“ wesentlich mehr, das heißt die Unterschiede sind für das geübte Ohr besser hörbar. Geiger spielen rein, während Klaviere notgedrungen temperiert spielen. Das Zusammenspiel ist daher zuweilen nicht unproblematisch, vor allem für geübte Ohren.

Musik und Mathematik sind auf vielfältige Weise miteinander verbunden, nicht nur in Harmonie, sondern auch in Rhythmus und Komposition.

B. Der Goldene Schnitt und Fibonacci

Der Goldene Schnitt, symbolisiert durch den griechischen Buchstaben Phi (φ ≈ 1.618), ist ein mathematisches Verhältnis, das als „göttliche Proportion“ bekannt ist und in der Natur, Kunst und Architektur häufig vorkommt. Es definiert sich als die Teilung einer Strecke in zwei Abschnitte, sodass das Verhältnis der gesamten Strecke zum längeren Abschnitt gleich dem Verhältnis des längeren Abschnitts zum kürzeren ist. Anders gesagt: Das Kleine zum Großen verhält sich wie das Große zum Ganzen.

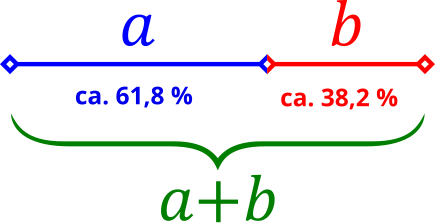
Nehmen wir an, die ganze Strecke habe die Länge 1 und ihr längeres Teilstück die Länge x, so führt vorige Forderung auf die Gleichung . Durch Multiplikation der Gleichung mit x erhalten wir daraus die quadratische Gleichung , beziehungsweise . Die einzig positive Lösung dieser Gleichung ist . Somit erhalten wir auch das Verhältnis des Ganzem zu den grüßenren Abscnitt, .

Der Ursprung des Goldenen Schnitts liegt in der griechischen Skulptur und Konstruktion. Viele Werke des berühmten Bildhauers Phidias (5. Jahrhundert v. Chr.) werden oft als Beispiele für die Verwendung des Goldenen Schnittes angesehen. Der Buchstabe φ wurde auch vor gut hundert Jahren  zu seinem Ehren eingeführt. Er wurde von Marcus Vitruvius Pollio (1. Jahrhundert v. Chr.), einem römischen Architekten und Ingenieur, in seinem Werk De architectura (Zehn Bücher über Architektur) ausführlich beschrieben. Vitruv vertrat die Ansicht, dass die perfekten Proportionen eines Gebäudes denen des idealen menschlichen Körpers entsprechen sollten. Er schreibt (am Anfang vom 3. Buch):

„Ferner ist natürlicherweise der Mittelpunkt des Körpers der Nabel. Liegt nämlich ein Mensch mit gespreizten Armen und Beinen auf dem Rücken, und setzt man die Zirkelspitze an der Stelle des Nabels ein und schlägt einen Kreis, dann werden von dem Kreis die Fingerspitzen beider Hände und die Zehenspitzen berührt. Ebenso, wie sich am Körper ein Kreis ergibt, wird sich auch die Figur eines Quadrats an ihm finden. Wenn man nämlich von den Fußsohlen bis zum Scheitel Maß nimmt und wendet dieses Maß auf die ausgestreckten Hände an, so wird sich die gleiche Breite und Höhe ergeben, wie bei Flächen, die nach dem Winkelmaß quadratisch angelegt sind.“

Leonardo da Vinci (1452–1519) illustrierte Vitruvs Beschreibung des idealen Menschen in seiner berühmten Zeichnung Vitruvianischer Mensch (ca. 1490), die einen nackten Mann mit ausgebreiteten Armen und Beinen darstellt, der gleichzeitig in einem Kreis und einem Quadrat eingeschrieben ist. Diese Zeichnung symbolisiert die Vereinigung von Kunst und Wissenschaft in der Renaissance. Vitruv behauptete, dass der Nabel und der Kopf vom Boden aus im Goldenen Schnitt zueinander stehen.

Der Goldene Schnitt ist eng mit der Fibonacci-Folge verbunden. Leonardo von Pisa (ca. 1170–1240), besser bekannt als Fibonacci, war ein einflussreicher Mathematiker des Mittelalters. In seinem Hauptwerk Liber Abaci (Buch der Rechenkunst) von 1202 führte er das indo-arabische Zahlensystem in Europa ein und stellte zahlreiche mathematische Probleme vor. Die Fibonacci-Folge (0, 1, 1, 2, 3, 5, 8, 13, …) leitet sich aus seinem berühmten Kaninchenproblem ab, das das Wachstum einer Kaninchenpopulation unter bestimmten Annahmen modelliert. Heute wissen wir, dass das Verhältnis aufeinanderfolgender Zahlen in der Fibonacci-Folge sich zunehmend dem Goldenen Schnitt annähert.

Der Goldene Schnitt ist in der Natur weit verbreitet, da viele Wachstumsprozesse, ähnlich dem Kaninchenbeispiel, diesem Verhältnis folgen. Dies ist in Schneckenhäusern, Sonnenblumen und anderen natürlichen Phänomenen zu beobachten. Auch in der Kunst, wie beispielsweise in „Las Meninas“ von Diego Velázquez, und in der griechischen Architektur finden sich zahlreiche Beispiele für die Anwendung des Goldenen Schnitts in der Komposition, was wahrscheinlich intuitiv als ästhetisch ansprechend empfunden wurde. Weitere berühmte Beispiele für die Komposition in goldenen Schnitt sind  “Das Mädchen mit dem Perlenohrring” von Vermeer, oder “Mona Lisa” von Leonardo.

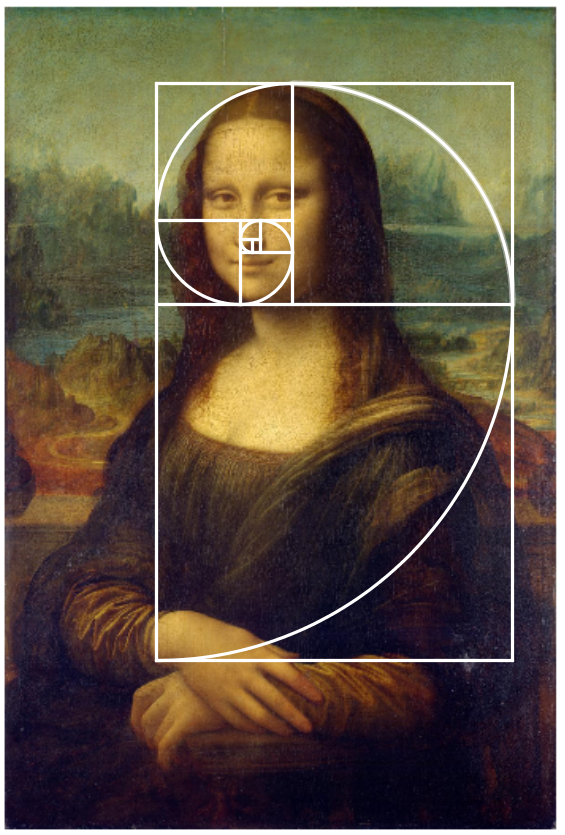
Das Pentagramm, ein regelmäßiges Fünfeck, enthält ebenfalls überall goldene Schnittverhältnisse. 

Interessanterweise findet der Goldene Schnitt auch Anwendung in der plastischen Chirurgie, wo Proportionen des Gesichts auf „Perfektion“ überprüft werden, um ideale Schönheitsstandards zu definieren. Sogenannte Reduktionszirkel werden verwendet, um die richtigen Verhältnisse, beispielsweise bei der Nasen- oder Kinnbreite, zu messen und anzupassen.

Dies wirft ethische Fragen auf, inwieweit solche Schönheitsideale durch Mathematik untermauert und der Gesellschaft aufgedrängt werden sollten. Ähnliche Anwendungen finden sich in der Schönheitszahnmedizin, wo Zähne geschliffen werden, um bestimmte Proportionen zu erreichen, die dem Goldenen Schnitt folgen. Es ist festzuhalten, dass viele Berühmtheiten, die allgemein als schön gelten, oft weit von diesen „mathematischen Idealen“ entfernt sind.

C. Darstellende Geometrie

Die darstellende Geometrie, insbesondere die perspektivische Darstellung, ist ein weiteres Feld, in dem Mathematik eine entscheidende Rolle für die Schönheit spielt. Systematische Ansätze zur Perspektive gab es bereits bei den Römern. In der Renaissance wurde die Linearperspektive mit ihren Fluchtpunkten systematisch erforscht und entwickelte sich zu einer hochentwickelten mathematischen Theorie.

Albrecht Dürer (1471–1528), ein bedeutender Künstler der Renaissance, war nicht nur für seine Gemälde und Gravuren bekannt, sondern auch für seine tiefgreifenden Studien der Geometrie und Perspektive. Er verfasste wichtige Geometriebücher, darunter „Underweysung der Messung mit dem Zirckel und Richtscheyt“ (1525), in denen er die Prinzipien der darstellenden Geometrie intensiv untersuchte, beispielsweise wie man mit geraden Linien nicht-gerade Formen erzeugen kann. Dürer verwendete Hilfsgitter, um seine Figuren präzise zu konstruieren. Die darstellende Geometrie findet sich in der Kunst reichlich wieder, insbesondere in barocken Tempeln mit ihren überfüllten perspektivischen Darstellungen.

D. Falsche Perspektiven und Fraktale

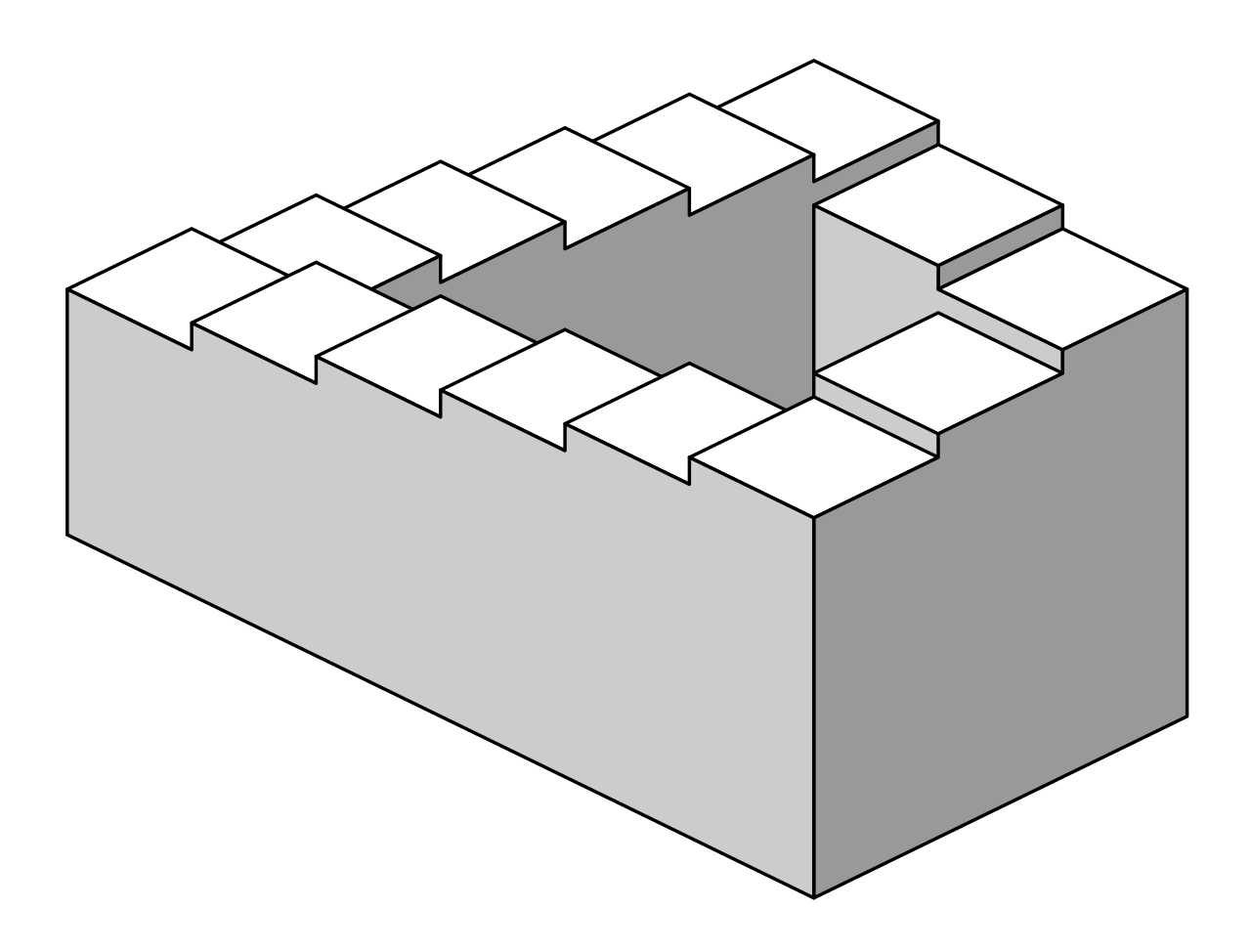
In der moderneren Kunst spielen auch bewusst „falsche Perspektiven“ eine Rolle. Maurits Cornelis Escher (1898–1972), ein niederländischer Grafiker, ist berühmt für seine Kunstwerke, die unmögliche Strukturen, optische Illusionen und unendliche Formen darstellen.

Eschers Arbeiten wurden von mathematischen Konzepten inspiriert, insbesondere von den „unmöglichen Objekten“ wie der Penrose-Treppe und dem Penrose-Dreieck, die von Roger Penrose (geb. 1931), einem britischen Mathematiker und Physiker (Nobelpreis der Physik 2020), zusammen mit seinem Vater entwickelt wurden. Escher nutzte auch die Theorie der Symmetriegruppen der Ebene, die von Mathematikern zur Charakterisierung von Kristallsymmetrien entwickelt wurde, um seine berühmten Parkettierungen zu schaffen.

Ein weiteres Beispiel für die Verbindung von Mathematik und Kunst sind Fraktale. Ein Fraktal ist eine geometrische Form, die detaillierte Strukturen auf beliebig kleinen Skalen aufweist und oft eine fraktale Dimension hat, die ihre topologische Dimension übersteigt. Viele Fraktale zeigen Selbstähnlichkeit, d.h., sie erscheinen auf verschiedenen Vergrößerungsstufen ähnlich. Der Begriff „Fraktal“ wurde 1975 von dem Mathematiker Benoît Mandelbrot geprägt. Die Mandelbrot-Menge ist ein klassisches und bekanntes Beispiel für ein Fraktal und hat sogar zu einer eigenen „Fraktalkunst“ geführt.

Schließlich sei noch das Klein-Modell für die hyperbolische Geometrie erwähnt, das von Felix Klein (1849–1925), einem deutschen Mathematiker, entwickelt wurde. Dieses Modell stellt einen nicht-euklidischen Raum dar, in dem eine Kreisscheibe der Raum ist und die Entfernungen so gemessen werden, dass sie vom Rand abhängen. Escher benutzte diese Idee auch öfter in seinen Abbildungen.

II. Schönheit der Mathematik

Die Frage nach der Schönheit der Mathematik selbst ist ein tiefgreifendes Thema. Trotz der Möglichkeit, mathematische Darstellungen oder Beweise „unschön“ zu gestalten, wird die „Grundmathematik an sich“ oft als inhärent schön empfunden.

Philosophen von der Antike bis zur Neuzeit haben die Schönheit der Mathematik diskutiert.

• Platon (ca. 428/427–348/347 v. Chr.) sah in Kreisen und Dreiecken die wahre Schönheit, da sie etwas Ewiges in sich tragen, im Gegensatz zu vergänglichen Dingen wie Frauen oder Blumen. Er empfand die Mathematik explizit als schön und diskutierte sie im Kontext der Schönheit (Timaios 53e, Philebos 51c).
• Aristoteles (384–322 v. Chr.) betonte in seiner Metaphysik, dass die Hauptformen der Schönheit „Ordnung und Symmetrie und Bestimmtheit“ sind, die die mathematischen Wissenschaften in besonderem Maße demonstrieren.
• Augustinus von Hippo (354–430 n. Chr.), ein einflussreicher christlicher Philosoph und Theologe, sah in Zahlen, Maß und Ordnung ein Abbild Gottes als Handwerker. Er argumentierte, dass mathematisches Wissen apriorisch ist und unsere intuitive Erkenntnis von Unendlichkeit nicht aus sinnlichen Erfahrungen stammen kann. Augustinus zufolge besitzt alles, was uns in materiellen Objekten gefällt und uns durch die Sinne anzieht, Zahl, und wir können nichts ohne „bestimmte Gesetze der Schönheit“ in uns beurteilen.
• Umberto Eco (1932–2016), ein italienischer Semiotiker und Philosoph, griff in seinem Roman Der Name der Rose (1980), aber auch in seinem kunsthistorisches Fachbuch Kunst und Schönheit im Mittelalter (1991) die platonische Idee auf, dass ein gleichseitiges Dreieck schöner ist als ein ungleichseitiges, da es mehr Gleichheit besitzt.

In der Mathematik wird ein „schönes Problem“ oft als ein schwieriges Problem beschrieben, während eine „schöne Lösung“ eine einfache, klare und elegante Lösung für ein komplexes Problem ist.

Ein bedeutender Vertreter der Mathematik im 20. Jahrhundert, Godfrey Harold Hardy (1877–1947), prägte in seinem Essay A Mathematician’s Apology (1940) die Ansicht, dass Mathematik eine Kunstform ist. Er verglich die Arbeit eines Mathematikers mit der eines Künstlers und betonte, dass man stets das Schönste suchen sollte, um wahre Erkenntnisse zu finden. Allerdings räumte er ein, dass die Schönheit der Mathematik nicht jedem zugänglich ist.

Es gibt zahlreiche Beispiele für Beweise in der Mathematik, die als schön empfunden werden können:

• Der Beweis der Winkelsumme im Dreieck durch Konstruktion, indem eine Hilfsgerade eingezeichnet wird, die Wechselwinkel erzeugt.
• Die Flächenformel eines Dreiecks mit Hilfe des Inkreises.
• Die Identität arctan(1/2​)+arctan(1/3​)=arctan(1)​.
• Geometrische Darstellungen unendlicher Reihen, wie z.B. 1/3=1/4+1/16+….

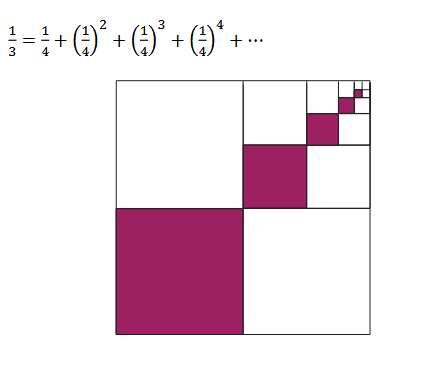
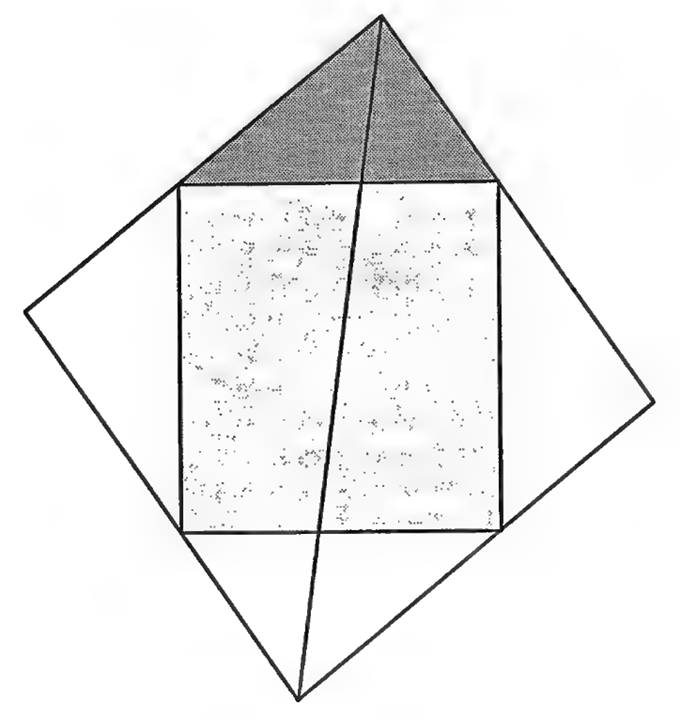
• Der Satz, der besagt, dass eine Gerade, die den rechten Winkel eines Dreiecks halbiert, das Quadrat an der Hypotenuse ebenfalls halbiert.

Der Mathematiker Pál Erdős hatte die einflussreiche platonische Auffassung, dass es ein himmlisches Buch geben soll, wo die perfekten, schönen Beweise der Mathematik gesammelt werden. Unsere Aufgabe ist es, nach diesen Beweisen zu streben. Nach seinem Tod haben Kollegen ein Buch der Beweise herausgegeben, wo er noch mitgewirkt hat. Solche beweise erzeugen in den Leser:innen ein Gefühl von Schönheit und Perfektion.

Im Schulunterricht gerät der künstlerische Aspekt der Mathematik oft in den Hintergrund, zugunsten einer Betonung ihrer Nützlichkeit. Besonders bei Kindern unter 14 Jahren ist jedoch festzustellen, dass Spaß und Schönheit oft eine höhere Motivation darstellen als bloße Nützlichkeit. Daher sollte der Mathematikunterricht, insbesondere in frühen Phasen, stärker auf diesen Aspekten basieren.

Zusammenfassend lassen sich zwei zentrale Botschaften hervorheben:

1. Verbindung von Kunst und Mathematik: Kunst und Mathematikunterricht sollten stärker miteinander verbunden werden. Dies zeigt, dass Mathematik nicht nur ein nützliches Werkzeug für Wirtschaft und Business ist, sondern ein integraler Bestandteil des menschlichen Schaffens und der Kultur.
2. Aufzeigen der Schönheit der Mathematik: Die inhärente Schönheit der Mathematik sollte im Schulunterricht stärker aufgezeigt werden. Ein rein lehrplanorientiertes Abarbeiten von Aufgaben verhindert das Erleben dieser Schönheit, die jedoch ein wichtiger Motivationsfaktor ist, da Menschen durch Schönheit und Freude stärker motiviert werden als durch bloße Nützlichkeit.

Literatur hierzu ist zwar vorhanden, aber nicht übermäßig umfangreich. Lehrpläne, wie der in Österreich, erwähnen die Schönheit der Mathematik kaum, im Gegensatz beispielsweise zu Nordrhein-Westfalen. Die Schule kann somit ein Ort sein, an dem Schönheitserfahrungen in der Mathematik gemacht werden können.

Ich bedanke mich bei Dr. Philipp Schöbi für verbesserungs- und Ergänzungsvorschläge.