Probleme (Vorlesung 10)

Herzlich willkommen zu unserer heutigen Vorlesung über die Herausforderungen und Errungenschaften in der Mathematik, die uns durch ungelöste und gelöste Probleme begegnen. Wie Sie wissen, ist die Mathematik eine dynamische und lebendige Wissenschaft, die sich durch das Stellen und Lösen von Problemen stetig weiterentwickelt hat. Bereits die ersten mathematischen Lehrwerke aus Mesopotamien und Ägypten waren im Kern Sammlungen von Aufgaben, deren Bearbeitung das Verständnis und die Entwicklung neuer Konzepte vorantrieb.

Dieser Vortrag ist so strukturiert, dass wir zunächst einige der bedeutendsten ungelösten Probleme der Mathematik betrachten, gefolgt von historischen Problemen, die im Laufe der Zeit gelöst wurden. Dabei werden wir auch einen Blick auf die Persönlichkeiten werfen, die sich diesen intellektuellen Herausforderungen stellten.

I. Ungelöste Probleme in der Mathematik

1. Die Collatz-Vermutung (3n+1-Problem)

Wir beginnen mit einem scheinbar einfachen, doch hartnäckig ungelösten Problem: der Collatz-Vermutung. Sie wurde 1937 von dem deutschen Mathematiker Lothar Collatz formuliert.

Lothar Collatz (1910–1990): Lothar Collatz wurde am 6. Juli 1910 in Arnsberg, Westfalen, geboren und verstarb am 26. September 1990 in Warna, Bulgarien. Er war ein deutscher Mathematiker, der sich auf Numerische Analysis spezialisierte und an verschiedenen deutschen Universitäten, darunter Greifswald, München, Göttingen und Berlin, studierte. Seinen Doktortitel erwarb er 1935 an der Universität Berlin mit einer Dissertation über Differenzenverfahren für lineare Differentialgleichungen. Collatz gründete 1953 das Institut für Angewandte Mathematik an der Universität Hamburg und war bis zu seiner Emeritierung 1978 dessen Leiter. Er erhielt zahlreiche Ehrungen, darunter die Aufnahme in die Deutsche Akademie der Naturforscher Leopoldina sowie Ehrendoktorwürden von mehreren Universitäten weltweit, wie der Universität São Paulo, der Technischen Universität Wien und der Universität Dundee.
Problemstellung: Man wählt eine beliebige natürliche Zahl n. Wenn n gerade ist, wird sie halbiert (n/2). Wenn n ungerade ist, wird sie mit 3 multipliziert und 1 addiert (3n+1). Die Collatz-Vermutung besagt, dass man, egal mit welcher positiven ganzen Zahl man beginnt, dieser Prozess immer bei der Zahl 1 endet. Die Sequenz wiederholt sich dann in einem Zyklus von 4, 2, 1.
Beispiel (Startwert n=7):
$7\rightarrow3\cdot7+1=22$
$22\rightarrow22/2=11$
$11\rightarrow3\cdot11+1=34$
$34\rightarrow34/2=17$
$17\rightarrow3 \cdot17+1=52$
$52\rightarrow52/2=26$
$26\rightarrow26/2=13$
$13\rightarrow3\cdot13+1=40$
$40\rightarrow40/2=20$
$20\rightarrow20/2=10$
$10\rightarrow10/2=5$
$5\rightarrow3\cdot5+1=16$
$16\rightarrow16/2=8$
$8\rightarrow8/2=4$
$4\rightarrow4/2=2$
$2\rightarrow2/2=1$

Obwohl das Problem leicht zu formulieren ist und Computer die Vermutung für immense Zahlen überprüft haben, bleibt sie bis heute ungelöst. Die Intuition, dass die Zahlenfolge immer größer werden müsste, bevor sie schließlich auf 1 zurückkehrt (da ungerade Zahlen stark vergrößert werden), macht die Stärke dieser Vermutung aus. Dieses Problem ist hervorragend geeignet, um bereits mit Kindern mathematisches Experimentieren zu fördern und dabei grundlegende Rechenfertigkeiten zu üben.

2. Primzahlzwillinge

Ein weiteres offenes Problem in der Zahlentheorie betrifft die Primzahlzwillinge.

Definition: Ein Primzahlzwilling ist ein Paar von Primzahlen $(p_1,p_2)$ , deren Abstand 2 beträgt, d.h., $p_2 -p_1=2$ . Beispiele sind (3, 5), (5, 7), (11, 13).
Problemstellung: Es ist bis heute unbekannt, ob es unendlich viele solcher Primzahlzwillingspaare gibt. Die Verteilung der Primzahlen ist ein zentrales Thema in der Zahlentheorie. Es ist bekannt, dass die Summe der Kehrwerte aller Primzahlen divergiert (Satz von Euler), was bedeutet, dass Primzahlen „dichter“ liegen als beispielsweise Quadratzahlen, deren Kehrwerte konvergieren. Die Kehrwerde alles Primzahlzwilinge konvergiert auch,dass ist die Brunsche Konstante. Trotzdem ist die Frage nach der Häufigkeit von Primzahlzwillingen offen.

3. Goldbachsche Vermutung

Die Goldbachsche Vermutung ist eine der bekanntesten ungelösten Probleme der Zahlentheorie.

Christian Goldbach (1690–1764): Christian Goldbach wurde am 18. März 1690 in Königsberg, Preußen (heute Kaliningrad, Russland), geboren und starb am 20. November 1764 in Moskau, Russland. Er war ein preußischer Mathematiker, der an der Universität Königsberg Jura, Medizin und Mathematik studierte. Nach ausgedehnten Reisen durch Europa, bei denen er Kontakt zu führenden Wissenschaftlern wie Gottfried Wilhelm Leibniz, Leonhard Euler, und Daniel Bernoulli pflegte, wurde er 1725 Professor für Mathematik und Historiker an der Kaiserlichen Akademie der Wissenschaften in St. Petersburg. Später war er auch als Tutor für den Zaren Peter II. tätig und arbeitete im russischen Außenministerium. Goldbach ist hauptsächlich für die nach ihm benannte Vermutung bekannt, die er 1742 in einem Brief an Leonhard Euler formulierte.
Problemstellung (Starke Goldbachsche Vermutung): Jede gerade Zahl größer als 2 kann als Summe von zwei Primzahlen geschrieben werden.
Beispiel (40): 40=3+37, 40=11+29, 40=17+23.
Problemstellung (Schwache Goldbachsche Vermutung): Jede ungerade Zahl größer als 5 kann als Summe von drei Primzahlen geschrieben werden.
Die schwache Goldbachsche Vermutung ist eine Folgerung der starken Goldbachschen Vermutung. In den letzten Jahrzehnten wurde für die schwache Goldbachsche Vermutung ein möglicher Beweis vorgelegt, der derzeit von der mathematischen Gemeinschaft intensiv geprüft wird. Die Komplexität des Beweises erfordert eine umfassende Überprüfung durch Experten, die Jahrelang andauert, es wird aber angenommen dass der Beweis korrekt sei.

Trotz umfangreicher numerischer Überprüfungen und der statistischen Beobachtung, dass größere Zahlen tendenziell mehr Primzahlzerlegungen zulassen, fehlt bis heute ein allgemeingültiger mathematischer Beweis für die starke Goldbachsche Vermutung.

4. Riemannsche Vermutung

Die Riemannsche Vermutung gilt als das vielleicht bedeutendste ungelöste Problem der Mathematik.

Bernhard Riemann (1826–1866): Bernhard Riemann war ein deutscher Mathematiker, der grundlegende Beiträge zur Analysis, Zahlentheorie und Differentialgeometrie leistete. Er ist bekannt für seine Arbeiten zur Riemannschen Zeta-Funktion, die eine entscheidende Rolle in der Verteilung der Primzahlen spielt.
Problemstellung: Die Riemannsche Vermutung ist eine Aussage über die Nullstellen der Riemannschen Zeta-Funktion. Sie besagt, dass alle nichttrivialen Nullstellen der Zeta-Funktion einen Realteil von 1/2 haben. Diese Vermutung ist von zentraler Bedeutung für das Verständnis der Verteilung der Primzahlen.
Primzahlsatz: Der Primzahlsatz, der 1896 bewiesen wurde (nach Vermutungen von Legendre und Gauß im späten 18. Jahrhundert), beschreibt die asymptotische Verteilung der Primzahlen. Er besagt, dass die Anzahl der Primzahlen $\pi(x)$ bis zu einer Zahl x sich annähert an $x/\ln(x)$ . Die Riemannsche Vermutung würde eine viel präzisere Abschätzung dieser Verteilung ermöglichen.
Bedeutung: Die Verteilung der Primzahlen ist von großer praktischer Relevanz, insbesondere in der modernen Kryptographie (z.B. RSA-Verfahren), wo die Sicherheit von Verschlüsselungen oft auf der Schwierigkeit basiert, große Primzahlen zu finden oder deren Produkte zu faktorisieren. Ein Beweis oder eine Widerlegung der Riemannschen Vermutung hätte tiefgreifende Auswirkungen auf die Sicherheit digitaler Kommunikation.

Die Komplexität des Problems liegt unter anderem in der Verwendung komplexer Funktionen und deren Nullstellen, ein Thema, das typischerweise erst in fortgeschrittenen Mathematikstudien behandelt wird.

5. Legendresche Vermutung

Adrien-Marie Legendre war ein französischer Mathematiker, der bedeutende Beiträge zu verschiedenen Bereichen leistete. Er ist bekannt für seine Arbeiten in der Zahlentheorie, insbesondere für die Legendresche Vermutung und den Legendreschen Dreieckssatz. Darüber hinaus beschäftigte er sich intensiv mit der Theorie der elliptischen Integrale und der Himmelsmechanik. Seine Werke umfassten auch wichtige Beiträge zur Theorie der Funktionen und zur Geometrie.

Problemstellung: Die Legendresche Vermutung besagt, dass zwischen $n^2$ und $(n+1)^2$ immer mindestens eine Primzahl liegt. Obwohl bekannt ist, dass Primzahlen in gewisser Weise dichter als Quadratzahlen verteilt sind (da die Summe der Kehrwerte der Primzahlen divergiert, während die der Quadratzahlen konvergiert), ist diese Vermutung bislang unbewiesen.

6. Vollkommene Zahlen

Definition: Eine vollkommene Zahl ist eine positive ganze Zahl, die gleich der Summe ihrer echten Teiler (also aller positiven Teiler außer der Zahl selbst) ist.
Beispiele: 6 (Teiler: 1, 2, 3; 1+2+3=6), 28 (Teiler: 1, 2, 4, 7, 14; 1+2+4+7+14=28), 496.
Problemstellung: Es ist ungelöst, ob es unendlich viele vollkommene Zahlen gibt und ob es eine ungerade vollkommene Zahl existiert. Alle bisher bekannten vollkommenen Zahlen sind gerade. Euklid bewies, dass $2^{k-1}(2^k-1)$ eine vollkommene Zahl ist, wenn $2^k-1$ eine Primzahl ist (sog. Mersenne-Primzahl). Euler bewies später, dass auf diese Weise alle geraden vollkommenen Zahlen erzeugt werden können.

7. Sophie-Germain-Primzahlen

Sophie Germain (1776–1831): Marie-Sophie Germain war eine bedeutende französische Mathematikerin, Physikerin und Philosophin. Sie leistete wichtige Beiträge zur Zahlentheorie und zur Theorie der Elastizität. Obwohl sie aufgrund ihres Geschlechts nicht formell an der École Polytechnique studieren durfte, korrespondierte sie unter Pseudonym mit führenden Mathematikern wie Lagrange und Gauß.
Definition: Eine Primzahl p heißt Sophie-Germain-Primzahl, wenn auch 2p+1 eine Primzahl ist.
Beispiele: 2 ist eine Sophie-Germain-Primzahl, da $2\cdot2+1=5$ prim ist. 3 ist eine Sophie-Germain-Primzahl, da $2\cdot3+1=7$ prim ist. 7 ist keine Sophie-Germain-Primzahl, da $2\cdot7+1=15$ nicht prim ist.
Problemstellung: Es ist nicht bekannt, ob es unendlich viele Sophie-Germain-Primzahlen gibt. Die Sophie-Germain-Primzahlen spielten bei der großen Fermatschen Satz eine wichtige Rolle (siehe unten).

8. Euler-Mascheroni-Konstante (γ)

Definition: Die Euler-Mascheroni-Konstante γ (Gamma) ist eine mathematische Konstante, die als Grenzwert der Differenz zwischen der harmonischen Reihe und dem natürlichen Logarithmus definiert ist:
$\gamma=\lim_{n\to\infty}\left(\sum_{k=1}^n\frac{1}{k}-\ln n \right) \approx 0,5772156649$ .
Problemstellung: Obwohl der Wert von gamma auf viele Dezimalstellen genau berechnet wurde, ist bis heute ungelöst, ob gamma eine rationale oder irrationale Zahl ist. Wenn sie rational wäre, müsste sie als Bruch zweier ganzer Zahlen darstellbar sein, was derzeit nicht bewiesen ist.

9. Erdös-Straus-Vermutung

Problemstellung: Die Erdös-Straus-Vermutung, benannt nach Paul Erdős und Ernst G. Straus, besagt, dass für jede natürliche Zahl $n\geq 2$ der Bruch 4/n als Summe von drei positiven Stammbrüchen geschrieben werden kann: $\frac{4}{n} = \frac{1}{a}+\frac{1}{b} + \\frac{1}{c}$ wobei a,b,c positive ganze Zahlen sind. Die Vermutung wurde 1948 aufgestellt und ist bis heute unbewiesen. Sie hat Beziehungen zu altägyptischen Zahlendarstellungen.

10. Problem von Brocard und Ramanujan

Srinivasa Ramanujan (1887–1920): Srinivasa Ramanujan war ein indischer Mathematiker, der trotz fehlender formaler Ausbildung außerordentliche Beiträge zur Analysis, Zahlentheorie, unendlichen Reihen und Kettenbrüchen leistete. Er korrespondierte mit dem englischen Mathematiker Godfrey Harold Hardy, der seine Genialität erkannte und ihn nach Cambridge holte. Seine Arbeiten und Vermutungen beeinflussen die Mathematik bis heute.
Problemstellung: Das Problem von Brocard und Ramanujan fragt nach den ganzzahligen Lösungen (n,m) der Gleichung n!+1=m².
Bekannte Lösungen: Die einzigen bekannten Lösungen sind für n=4,m=5 (4!+1=24+1=25=5²), für n=5,m=11 (5!+1=120+1=121=11²) und für n=7,m=71 (7!+1=5040+1=5041=71²). Es wird vermutet, dass dies die einzigen Lösungen sind.

11. Taxicab-Zahlen (Hardy-Ramanujan-Zahlen)

Problemstellung: Eine Taxicab-Zahl Ta(n) ist die kleinste positive ganze Zahl, die auf n verschiedene Arten als Summe von zwei positiven Kubikzahlen (a³+b³) dargestellt werden kann.
Bekannte Taxicab-Zahlen:

Ta(1)=2=1³+1³
Ta(2)=1729=1³+12³=9³+10³. Diese Zahl ist bekannt aus einer Anekdote über Godfrey Harold Hardy, der Ramanujan im Krankenhaus besuchte und 1729 als „langweilig“ bezeichnete, woraufhin Ramanujan die interessante Eigenschaft der Zahl aufzeigte.
Weitere Taxicab-Zahlen bis Ta(6) sind bekannt. Es ist unklar, ob die Liste unendlich ist.

12. P versus NP Problem

Problemstellung: Dies ist ein zentrales ungelöstes Problem der theoretischen Informatik und Mathematik, das sich mit der Klassifizierung von Rechenproblemen beschäftigt.

P (Polynomialzeit): Die Klasse P umfasst alle Entscheidungsprobleme, für die ein deterministischer Algorithmus existiert, der sie in Polynomialzeit lösen kann. Das bedeutet, die Anzahl der Rechenschritte des Algorithmus wächst polynomial mit der Größe der Eingabe. Probleme in P gelten als „einfach“ oder „effizient“ lösbar.
NP (Nichtdeterministische Polynomialzeit): Die Klasse NP umfasst alle Entscheidungsprobleme, deren Lösungen, wenn sie gegeben sind, in Polynomialzeit verifiziert werden können. Dies bedeutet, dass, wenn jemand eine potenzielle Lösung präsentiert, man schnell überprüfen kann, ob diese korrekt ist. Es ist unklar, ob NP-Probleme auch in Polynomialzeit gelöst werden können, also ob P=NP ist.

Bedeutung: Die Frage, ob P = NP, hat weitreichende Implikationen für die Informatik, Kryptographie und viele andere Bereiche. Wenn P=NP wäre, könnten viele heute als „schwer“ geltende Probleme (wie das Problem des Handlungsreisenden oder die Entschlüsselung vieler moderner Kryptosysteme) effizient gelöst werden. Die allgemeine Vermutung ist jedoch, dass P neq NP ist, obwohl dies bisher unbewiesen ist.
Problem des Handlungsreisenden: Dies ist ein klassisches Beispiel für ein NP-schweres Problem. Es geht darum, für eine gegebene Menge von Städten und den Entfernungen zwischen ihnen den kürzesten möglichen Weg zu finden, der jede Stadt genau einmal besucht und zum Ausgangspunkt zurückkehrt. Praktische Anwendungen finden sich in der Logistik, Tourenplanung und Paketlieferung. Es ist ein „NP-hartes“ Problem, was bedeutet, dass es mindestens so schwer ist wie jedes NP-Problem.

II. Gelöste Probleme in der Mathematik

1. Vier-Farben-Satz

Problemstellung: Der Vier-Farben-Satz besagt, dass jede ebene Landkarte mit höchstens vier Farben so gefärbt werden kann, dass benachbarte Länder (die eine gemeinsame Grenze haben, nicht nur einen Punkt) unterschiedliche Farben aufweisen. Die Vermutung wurde erstmals 1852 aufgestellt. Das man mindestens vier Farben braucht, sieht man schnell bei der Karte .
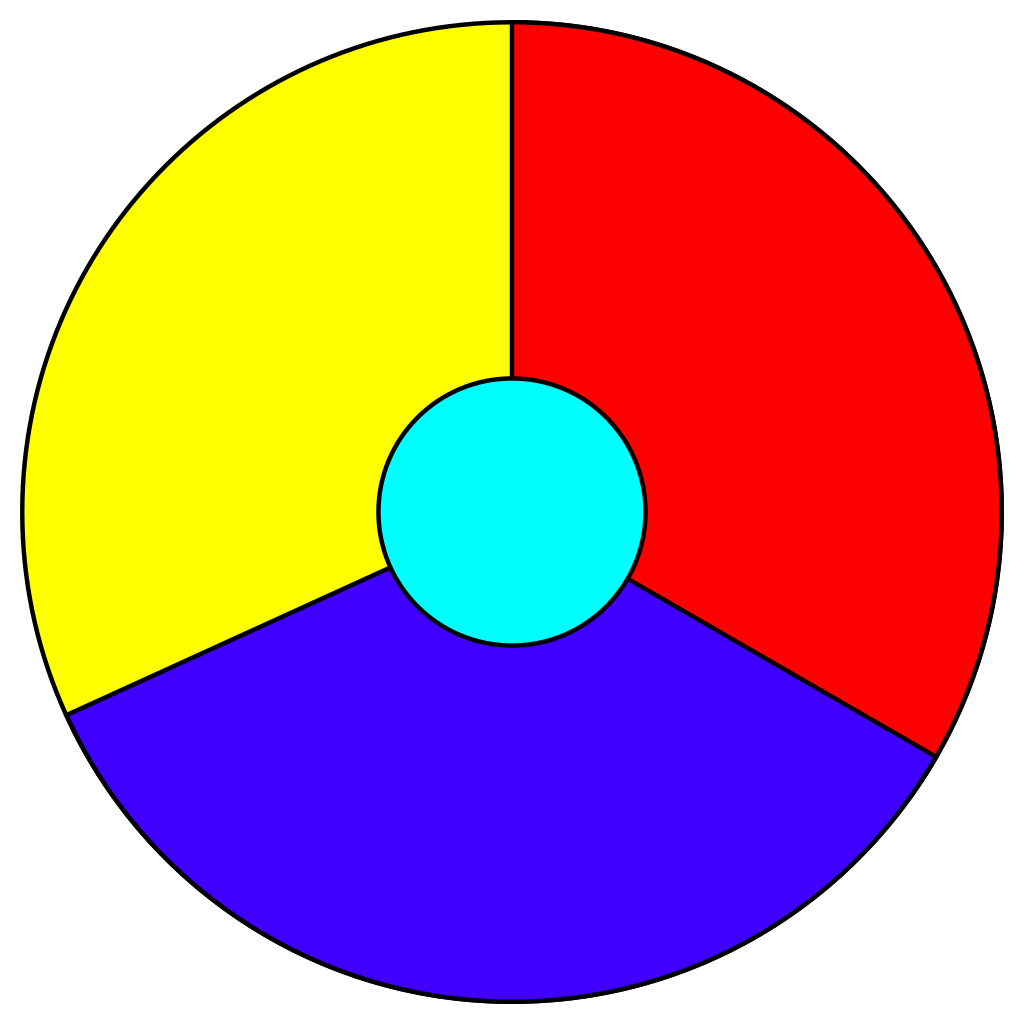Lösung: Der Vier-Farben-Satz wurde 1976 von Kenneth Appel und Wolfgang Haken an der University of Illinois bewiesen. Dies war der erste bedeutende mathematische Satz, dessen Beweis maßgeblich durch den Einsatz von Computern erfolgte. Der Beweis umfasste die Reduktion des Problems auf eine endliche Anzahl von Konfigurationen, die dann systematisch von einem Computer überprüft wurden (mehr als tausend Fälle). Die Abhängigkeit von Computerberechnungen führte zu philosophischen Debatten über die Natur mathematischer Beweise.

2. Satz von Abel-Ruffini

Problemstellung: Seit der Antike suchten Mathematiker nach allgemeinen Formeln zur Lösung von Polynomgleichungen. Für Gleichungen bis zum vierten Grad (linear, quadratisch, kubisch, quartisch) waren solche Formeln bekannt. Die Frage war, ob dies auch für Polynomgleichungen höheren Grades zutrifft.
Lösung: Der Satz von Abel-Ruffini besagt, dass es keine allgemeine Lösungsformel für Polynomgleichungen vom Grad fünf oder höher gibt, die nur arithmetische Operationen (Addition, Subtraktion, Multiplikation, Division) und Wurzelausdrücke verwendet. Dies wurde unabhängig voneinander von Paolo Ruffini (ca. 1799) und Niels Henrik Abel (1824) bewiesen. Der Beweis stützt sich auf Konzepte der Gruppentheorie, insbesondere der Galois-Theorie.

3. Satz von Bolyai-Gerwien

Problemstellung: In der Geometrie stellt sich die Frage, ob zwei flächengleiche Polygone durch Zerlegung in endlich viele kongruente Teile ineinander überführt werden können.
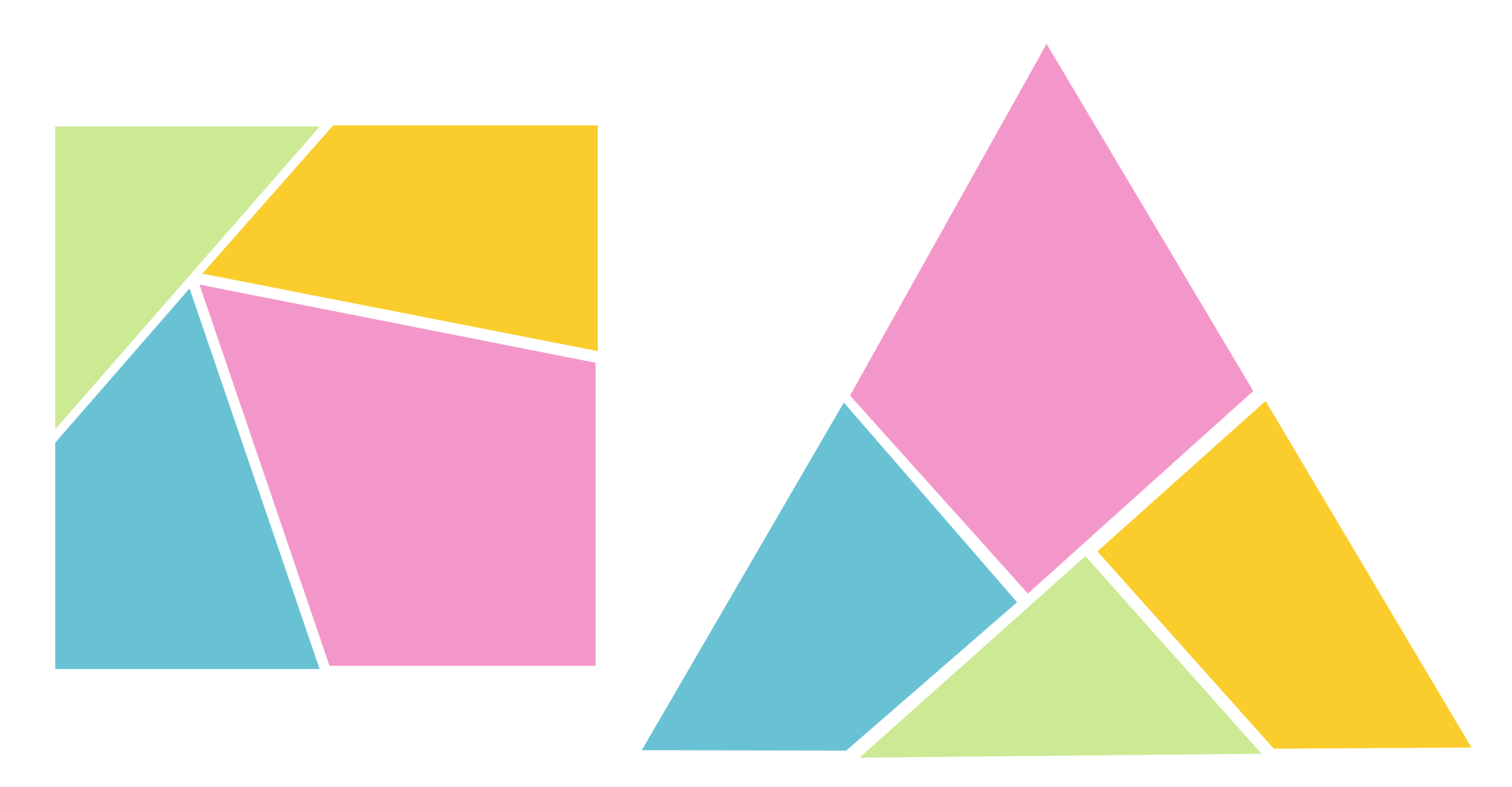
Lösung: Der Satz von Bolyai-Gerwien (benannt nach Farkas Bolyai und Paul Gerwien) wurde 1833 bewiesen und besagt, dass zwei flächengleiche Polygone stets zerlegungsgleich sind, d.h., das eine kann in endlich viele Polygonteile zerlegt werden, die sich zum anderen Polygon zusammensetzen lassen. Hilbert stellte 1900 die Frage, ob ein analoger Satz auch in drei Dimensionen für Polyeder gilt. Dieses Problem (Hilberts drittes Problem) wurde 1900 von Max Dehn negativ beantwortet: Es gibt zwei volumen-gleiche Tetraeder, die nicht zerlegungsgleich sind.

4. Großer Fermatscher Satz

Pierre de Fermat (1601–1665): Pierre de Fermat war ein französischer Jurist und Amateurmathematiker, der bedeutende Beiträge zur Zahlentheorie leistete. Er ist bekannt für seine Vermutungen, von denen die bekannteste der Große Fermatsche Satz ist.
Problemstellung: In seinem Exemplar von Diophantus‘ „Arithmetica“ notierte Fermat um 1637 am Seitenrand, dass die Gleichung aⁿ+bⁿ=cⁿ für ganze Zahlen a,b,c>0 und für ganze Zahlen n>2 keine Lösung hat. Er behauptete, einen „wunderbaren Beweis“ gefunden zu haben, für den der Rand jedoch zu klein sei. Über 350 Jahre lang blieb dieser Satz unbewiesen und faszinierte Mathematiker weltweit, während erfolglose Lösungsversuche die Entwicklung neuer mathematischer Theorien vorantrieben.
Lösung: Der Große Fermatsche Satz wurde 1994 von Andrew Wiles, einem britischen Mathematiker, bewiesen. Sein Beweis, der auf einer Reihe tiefgreifender Arbeiten in der Zahlentheorie und elliptischen Kurven aufbaut, war eine der größten mathematischen Errungenschaften des 20. Jahrhunderts.

5. Klassische Griechische Konstruktionsprobleme

Die alten Griechen stellten drei berühmte Probleme der Geometrie, die sie versuchten, nur mit Zirkel und Lineal zu lösen:

Quadratur des Kreises: Die Aufgabe, ein Quadrat zu konstruieren, das den gleichen Flächeninhalt wie ein gegebener Kreis besitzt.
Lösung: Die Unmöglichkeit der Quadratur des Kreises wurde 1882 von Ferdinand von Lindemann bewiesen, der zeigte, dass die Kreiszahl pi eine transzendente Zahl ist. Da Konstruktionen mit Zirkel und Lineal nur Lösungen von Polynomgleichungen mit rationalen Koeffizienten liefern können, und transzendente Zahlen per Definition keine solchen Polynomgleichungen erfüllen, ist die Quadratur des Kreises unmöglich.
Würfelverdopplung (Delisches Problem): Die Aufgabe, einen Würfel zu konstruieren, dessen Volumen doppelt so groß ist wie das eines gegebenen Würfels.
Lösung: Die Unmöglichkeit der Würfelverdopplung mit Zirkel und Lineal wurde im 19. Jahrhundert bewiesen. Die Seitenlänge eines solchen Würfels wäre $\sqrt[3]{2}$ mal so groß wie die ursprüngliche Seitenlänge. Da $\sqrt[3]{2}$ keine konstruierbare Zahl ist (d.h., sie kann nicht als Lösung einer Folge von quadratischen Gleichungen dargestellt werden), ist die Konstruktion unmöglich.
Dreiteilung des Winkels: Die Aufgabe, einen beliebigen Winkel mit Zirkel und Lineal in drei gleiche Teile zu teilen.
Lösung: Die allgemeine Dreiteilung des Winkels wurde im 19. Jahrhundert ebenfalls als unmöglich erwiesen. Dies liegt daran, dass die Konstruktion im Allgemeinen die Lösung einer kubischen Gleichung erfordern würde, die nicht immer mit Zirkel und Lineal gelöst werden kann.

6. Keplersche Vermutung

Problemstellung: Die Keplersche Vermutung besagt, dass die dichteste Packung von gleich großen Kugeln im dreidimensionalen Raum diejenige ist, die einem Kugelpackungskoeffizienten von etwa 74,05% entspricht, wie er bei der kubisch-flächenzentrierten oder hexagonalen Packung erreicht wird. Dies entspricht der intuitiven Anordnung von Orangen in einer Kiste.
Lösung: Die Vermutung wurde 1998 von Thomas Hales mittels einer Kombination aus mathematischem Beweis und umfangreichen Computerberechnungen bewiesen. Eine formelle Verifikation des Beweises durch das Projekt „Flyspeck“ wurde 2014 abgeschlossen.

7. Catalansche Vermutung

Problemstellung: Die Catalansche Vermutung besagt, dass x^a−y^b=1 die einzige Lösung in natürlichen Zahlen x,a,y,b>1 hat, die x=3, a=2, y=2, b=3 ist (d.h. 3²−2³=9−8=1).
Lösung: Die Catalansche Vermutung wurde 2002 von Preda Mihăilescu vollständig bewiesen. Schon Euler zeigte, dass die Gleichung a²–b³ = 1 nur die Lösungen a=3, b=2 haben kann.

8. Poincaré-Vermutung

Henri Poincaré (1854–1912): Henri Poincaré war ein französischer Mathematiker, Physiker und Philosoph der Wissenschaft. Er leistete Pionierarbeit in der Topologie, einem Teilgebiet der Mathematik, das er mitbegründete.
Problemstellung: Die Poincaré-Vermutung ist eine fundamentale Aussage in der Topologie. Sie besagt, dass jede einfach zusammenhängende, geschlossene 3-dimensionale Mannigfaltigkeit homöomorph zur 3-Sphäre ist. Anschaulich bedeutet dies, dass jedes dreidimensionale Objekt ohne Löcher oder Ränder, das in jeder Schleife zusammengezogen werden kann (wie die Oberfläche einer Kugel), topologisch äquivalent zu einer 3-dimensionalen Kugel ist.
Lösung: Die Poincaré-Vermutung, die 1904 von Henri Poincaré formuliert wurde, wurde 2002 von Grigori Perelman bewiesen. Er veröffentlichte seinen Beweis nicht in traditionellen Fachzeitschriften, sondern auf arXiv. Perelman lehnte den Fields-Medaille und den Millennium-Preis des Clay Mathematics Institute ab.

9. Apéry-Konstante (ζ(3))

Roger Apéry (1916–1994): Roger Apéry war ein griechisch-französischer Mathematiker.
Problemstellung: Die Werte der Riemannschen Zeta-Funktion ζ(s) für gerade positive ganze Zahlen s waren bereits von Euler bekannt (z.B. ζ(2)= $\pi$ ²/6). Für ungerade positive ganze Zahlen war die Natur der Werte jedoch lange Zeit unbekannt. Insbesondere war die Rationalität oder Irrationalität von ζ(3) eine offene Frage.
Lösung: 1978 bewies Roger Apéry, dass ζ(3) (die Apéry-Konstante) eine irrationale Zahl ist. Dieser Beweis war überraschend, da Apéry nicht zu den bekanntesten Mathematikern seiner Zeit gehörte und sein Beweis eine neue Methode einführte.
Transzendente und Irrationale Zahlen:

Irrationalität von pi und e: Die Irrationalität von pi wurde 1761 von Johann Heinrich Lambert bewiesen. Die Irrationalität von e wurde 1737 von Leonhard Euler bewiesen.
Transzendenz von π und e: Die Transzendenz von π wurde 1882 von Ferdinand von Lindemann bewiesen. Die Transzendenz von e wurde 1873 von Charles Hermite bewiesen. Eine transzendente Zahl ist eine Zahl, die nicht Nullstelle eines Polynoms mit rationalen Koeffizienten ist. Dies impliziert, dass π und e nicht als Wurzeln einer algebraischen Gleichung darstellbar sind.

Fazit

Die Mathematik ist eine Disziplin, die sich durch die Formulierung und das Streben nach Lösungen für komplexe Probleme kontinuierlich weiterentwickelt. Die hier vorgestellten ungelösten und gelösten Probleme illustrieren nicht nur die intellektuelle Tiefe des Faches, sondern auch seine dynamische Natur. Es ist entscheidend, im Mathematikunterricht nicht nur fertige Lösungen zu präsentieren, sondern auch die Existenz offener Fragen zu thematisieren. Dies vermittelt ein realistischeres Bild der Mathematik als einer lebendigen Wissenschaft, in der es noch viel zu entdecken gibt. Das Experimentieren mit mathematischen Konzepten, auch bei scheinbar einfachen Problemen wie der Collatz-Vermutung, fördert nicht nur das rechnerische Geschick, sondern auch die Kreativität und die Fähigkeit zur eigenständigen Problemlösung. Viele Probleme, die einst als unüberwindbar galten, wurden durch neue Theorien und innovative Ansätze gelöst, oft nach Jahrhunderten der Forschung. Dies zeigt, dass Hartnäckigkeit und die Weiterentwicklung mathematischer Werkzeuge zum Erfolg führen können, selbst wenn die ursprünglichen Problemsteller keine Lösung fanden.

András Bátkai's Weblog