András Bátkai's Weblog

Die zentrale Rolle des Problemlösens in der Mathematik

Was ich heute mit Ihnen besprechen möchte, sind einige zentrale Aspekte des Problemlösens in der Mathematik. Problemlösen ist ein fundamentaler Begriff, der die Essenz der Mathematik ausmacht. Viele Mathematiker und Pädagogen sind der Ansicht, dass Theorien, Definitionen und Konzepte primär existieren, um uns die Werkzeuge an die Hand zu geben, mit denen wir Probleme analysieren, verstehen und letztendlich lösen können. Für den Mathematikunterricht bedeutet dies, dass die Vermittlung von Problemlösekompetenzen ein vorrangiges Ziel sein sollte.

Diese Überzeugung ist keineswegs neu, sondern tief in der Geschichte der Mathematik verwurzelt. Schon die ältesten bekannten mathematischen Texte aus Mesopotamien und dem alten Ägypten waren Sammlungen von Aufgaben, die zur Ausbildung von Schülerinnen und Schülern dienten. Seit der Verschriftlichung der Mathematik, also seit den frühesten Zeugnissen schriftlicher mathematischer Praxis, spielte das Lösen von Aufgaben und Problemen eine zentrale Rolle in der Disziplin und ihrer Vermittlung.

Ein klassisches Beispiel hierfür sind die Werke Euklids. Typischerweise wurden seine Bücher nicht nur gelesen, sondern aktiv studiert, indem man versuchte, die formulierten Theoreme selbst zu beweisen, anstatt sich lediglich die vorgegebenen Lösungen anzusehen. Es gibt sogar Beispiele aus Euklids Zeit, die zeigen, dass Gelehrte seine Sätze auf ihre eigene Art zu lösen versuchten, was sich in abweichenden Bildern und Formulierungen in den überlieferten Texten widerspiegelt. Selbst nach der Erfindung des Buchdrucks, der billigere Buchausgaben ermöglichte, wurden spezielle Studentenausgaben von Euklids Elementen angefertigt, in denen die Beweise bewusst weggelassen wurden. Dies machte die Bücher dünner und kostengünstiger, aber vor allem zwang es die Lernenden dazu, die Beweise selbst zu erarbeiten. Dies unterstreicht, dass das Mathematiklernen niemals eine passive Aktivität war, sondern stets ein aktiver Prozess, der Bemühung und Anstrengung erforderte, um zu wirklichem Verständnis und Erfolg zu gelangen.

Leider ist dieses Verständnis auch heute noch nicht überall im Mathematikunterricht etabliert. Oft herrscht die falsche Vorstellung, dass die Aufgabe der Lehrperson darin bestünde, lediglich gute Erklärungen zu liefern, die von den Schülern passiv konsumiert werden können. Doch allein durch passives Zuschauen kann niemand wirklich lernen. Echtes Verständnis erfordert aktive Auseinandersetzung und eigene Erarbeitung. Die Erwartungshaltung, wie im Kino passiv dabei zu sein und nur bei Unklarheiten „Ich verstehe es nicht!“ zu rufen, ist weit verbreitet, aber kontraproduktiv. Die Geschichte des Mathematikunterrichts zeigt, dass Lernen immer eine persönliche Erarbeitung und ein aktives Verstehen war.

George Pólya: Ein Leben im Dienste des Problemlösens

An dieser Stelle möchte ich über eine Schlüsselfigur sprechen, die das Problemlösen in der Mathematik und ihrer Didaktik maßgeblich geprägt hat: George Pólya. Es wird oft gesagt, dass die philosophischen oder didaktischen Ansätze eines Menschen stark von seinem Lebensweg und seinen Erfahrungen beeinflusst werden. Daher werfen wir einen kurzen Blick auf Pólyas Biografie.

George Pólya wurde am 13. Dezember 1887 in Budapest, Österreich-Ungarn, geboren und starb am 7. September 1985 in Palo Alto, USA. Er war ein ungarischer Mathematiker, der später auch die Schweizer und US-amerikanische Staatsbürgerschaft annahm. Interessanterweise begann seine akademische Laufbahn nicht direkt mit Mathematik. Er studierte ursprünglich Philologie, wollte aber wegen der Philosophie auch einige Physik- und Mathematikkurse belegen. Da ihm dies aufgrund damaliger Restriktionen bei Fächerkombinationen verwehrt wurde, entschied er sich aus Zorn, ausschließlich Mathematik und Physik zu studieren. So wurde er relativ spät zu einem bedeutenden Mathematiker.

Pólya avancierte schnell zu einem renommierten Problemlöser und wurde Professor an der ETH Zürich, bevor er in den frühen 1940er Jahren nach Stanford, USA, wechselte. Er gilt als einer der Begründer der modernen Wahrscheinlichkeitstheorie. Seine Arbeitsgebiete umfassten insbesondere Wahrscheinlichkeitstheorie, Analysis, Kombinatorik und Zahlentheorie.

Zu seinen wichtigen Beiträgen zählen unter anderem:

• Er hat an extrem gelesenen Fachbüchern mitgewirkt, wie Pólya-Szegő oder Hardy-Littlewood-Pólya.
• Zentraler Grenzwertsatz: Er prägte diesen Begriff im Jahr 1920 in einer sehr einflussreichen Publikation.
• Satz von Pólya über Irrfahrten: 1921 bewies er diesen berühmten Satz, der besagt, dass ein Punkt A in einem D-dimensionalen ganzzahligen Gitter ZD von einer vom Ursprung ausgehenden Irrfahrt nur in D=1,2 mit Wahrscheinlichkeit 1 erreicht wird, während dies in mehr Dimensionen nur mit Wahrscheinlichkeit kleiner 1 geschieht. Ein anschauliches Beispiel hierfür ist der „betrunkene Spaziergänger“, der zufällig nach links oder rechts geht und die Frage, ob er irgendwann zum Ausgangspunkt zurückkehrt. Der Mathematiker Kakutani hat den Satz folgendermaßen kommentiert: „A drunk man will find his way home, but a drunk bird may get lost forever“.
• Charakteristische Funktionen: 1918 beschrieb Pólya in der Wahrscheinlichkeitstheorie die charakteristischen Funktionen.
• Eindeutigkeit von Wahrscheinlichkeitsmaßen: 1923 zeigte er, dass Wahrscheinlichkeitsmaße eindeutig festliegen.
• Abzählsatz von Pólya: Dieser Satz aus der enumerativen Kombinatorik ermöglicht das Abzählen von Strukturen wie Bäumen, Graphen oder chemischen Verbindungen unter Berücksichtigung von Symmetrien.
• Fueter-Pólya-Vermutung: Eine wichtige, bis heute ungelöste Vermutung, die Pólya gemeinsam mit Rudolf Fueter aufstellte und die sich mit gewissen Polynomen und Zahlentheorie befasst.
• Pólya-Verteilung: Eine diskrete Wahrscheinlichkeitsverteilung, die seinen Namen trägt und in der Stochastik Anwendung findet. Man könnte damit Krankheitverbreitung modellieren.
• Kristallsymmetrie in der Ebene: Pólya schrieb eine bedeutende Arbeit über die Analogie der Kristallsymmetrie in der Ebene, die er parallel zu den Arbeiten von PAil Niggli entwickelte. Diese Arbeiten hatten einen direkten Einfluss auf M.C. Escher, dessen berühmte Parkettierungen, wie die des Vogels, auf diesen mathematischen Symmetrien basieren und die Verbindung zwischen Mathematik und Kunst aufzeigen. Im Folgenden sehen wir die Abbildungen aus Pólyas Arbeit (links) und die Notizen von Escher dazu.

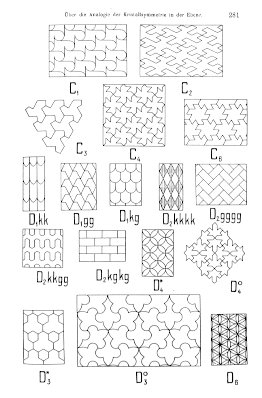
• Pferde-Paradox: Obwohl es sich um ein Scheinparadox handelt, das auf der fehlerhaften Anwendung der vollständigen Induktion beruht, wird es oft George Pólya zugeschrieben. Es veranschaulicht, dass alle Pferde dieselbe Farbe haben müssten, wenn man die Induktion falsch anwendet. Der Fehler liegt hierbei im Induktionsschritt von n=1 auf n=2, wo die Überlappung der Mengen nicht gegeben ist.

Pólya war ein äußerst produktiver Mathematiker, der in verschiedenen Bereichen tätig war und hauptsächlich Probleme löste. Er reflektierte nicht nur über das Problemlösen, sondern recherchierte auch ausführlich die Ansichten früherer Autoren dazu. Seine Arbeit bildet bis heute die Grundlage der Didaktik des Problemlösens.

Pólyas Heuristik des Problemlösens: Ein Leitfaden für Denken und Lehren

Pólya widmete sich früh dem Problemlösen und verfasste sogar einen Aufsatz für Lehrer zu diesem Thema. Er schrieb mehrere ausgezeichnete Bücher zum Problemlösen, doch sein bekanntestes Werk ist „Schule des Denkens. Vom Lösen mathematischer Probleme„, das 1945 erschien. Dieses Buch gilt als hervorragender Einstieg in das Thema. Andere seiner Werke vertiefen spezifische Aspekte des Problemlösens und enthalten zahlreiche Aufgaben mit Lösungen sowie didaktische Überlegungen für den Unterricht.

Pólya strukturierte den Problemlöseprozess in vier Phasen, die zwar oft diskutiert und manchmal auch kritisiert werden, weil sie das menschliche Denken nicht starr kategorisieren können. Doch Pólya selbst sah sie nicht als starre Abfolge, sondern als identifizierbare Phasen, die durch gezielte Fragestellungen unterstützt werden können. Implizit war er ein Verfechter dessen, was man heute als sokratische Methode bezeichnet. Man lässt die Kinder etwas entdecken, aber nicht „freies Entdecken“, wie man es vom entdeckenden Lernen annimmt, sondern man kommt in einem Dialog mit den Kindern und, wie Sokrates das immer gemacht hat, lässt man sie mit gezielten, guten Fragen selbst darauf kommen. Dadurch entsteht beim Schüler das Gefühl, die Lösung selbst gefunden zu haben, auch wenn er geleitet wurde.

Die vier Phasen des Problemlösens nach Pólya sind (Die Hilfsfragen zitieren wir aus seinem Buch):

1. Die Aufgabe verstehen (Understanding the Problem): Diese Phase wird oft unterschätzt. Viele beginnen sofort mit dem Lösen, ohne die Aufgabe richtig durchzulesen. Es ist entscheidend zu klären, was bekannt, was gegeben und was unbekannt ist. Bei einfachen Aufgaben führt ein gründliches Verstehen oft direkt zur Lösung. Pólya schlägt gezielte Fragen für diese Phase vor:

• Was ist bekannt? Was ist gegeben? Wie lautet die Bedingung?
• Ist es möglich, die Bedingung zu befriedigen? Ist die Bedingung ausreichend, um die Unbekannte zu bestimmen? Oder ist sie unzureichend? Oder überbestimmt?
• Zeichne eine Figur! Führe eine passende Bezeichnung ein!
• Trenne die verschiedenen Teile der Bedingung! Kannst Du sie formulieren?

2. Einen Plan entwickeln (Devising a Plan): Hier geht es darum, eine Strategie zur Lösung zu finden. Pólya empfiehlt, sich zu fragen:

• Hast Du die Aufgabe schon früher gesehen? Oder hast Du dieselbe Aufgabe in einer wenig verschiedenen Form gesehen?
• Kennst Du eine verwandte Aufgabe? Kennst Du einen Lehrsatz, der förderlich sein könnte?
• Betrachte die Unbekannte! Und versuche, Dich auf eine Dir bekannte Aufgabe zu besinnen, die dieselbe oder eine ähnliche Unbekannte hat.
• Hier ist eine Aufgabe, die der Deinen verwandt und schon gelöst ist. Kannst Du sie gebrauchen? Kannst Du ihr Resultat verwenden? Kannst Du ihre Methode verwenden? Würdest Du irgendein Hilfselement einführen, damit Du sie verwenden kannst?
• Kannst Du die Aufgabe anders ausdrücken? Geh auf die Definition zurück!
• Wenn Du die vorliegende Aufgabe nicht lösen kannst, so versuche, zuerst eine verwandte Aufgabe zu lösen. Kannst Du Dir eine zugänglichere verwandte oder allgemeinere, oder spezielle, oder analoge Aufgabe denken?
• Kannst Du einen Teil der Aufgabe lösen? Behalte nur einen Teil der Bedingung bei und lasse den anderen fort; wie weit ist die Unbekannte dann bestimmt, wie kann ich sie verändern?
• Kannst Du Dir andere Daten denken, die geeignet sind, die Unbekannte zu bestimmen?
• Hast Du die ganze Bedingung benutzt? Hast Du alle wesentlichen Begriffe in Rechnung gezogen, die in der Aufgabe enthalten sind?

Diese Fragen sind so formuliert, dass sie die Denkprozesse anregen, ohne zu stark zu lenken. Für Lehrpersonen ist es ratsam, sich solche Fragen bei der Vorbereitung auf Aufgaben zu überlegen, um den Schülerinnen und Schülern gezielt Hilfestellung geben zu können. Problemlöseheuristiken wie Verallgemeinern, Spezialisieren, Vorwärts- und Rückwärtsarbeiten können systematisch trainiert werden.

3. Den Plan ausführen (Carrying out the Plan): In dieser Phase wird der entwickelte Plan in die Tat umgesetzt. Hierbei ist es entscheidend, jeden Schritt sorgfältig zu kontrollieren und zu überprüfen.

• Kontrolliere jeden Schritt!
• Kannst Du deutlich sehen, dass der Schritt richtig ist? Kannst Du beweisen, dass er richtig ist?

4. Rückschau halten (Looking Back): Nach dem Lösen der Aufgabe ist es wichtig, die Lösung zu überprüfen und den Lösungsweg zu reflektieren.

• Kannst Du das Resultat kontrollieren? Kannst Du den Beweis kontrollieren?
• Kannst Du das Resultat auf verschiedene Weise ableiten? Kannst Du es auf den ersten Blick sehen?
• Kannst Du das Resultat oder die Methode für irgendeine andere Aufgabe gebrauchen? Die Suche nach alternativen Lösungswegen ist ein wichtiges Merkmal guter Aufgaben.

Die Diskussion über die wichtigen Schritte und ihre Übertragbarkeit auf andere Aufgaben fehlt oft im Unterricht.

Anwendungsbeispiel: Die Kartenhausaufgabe

Betrachten wir die Kartenhausaufgabe, um Pólyas Phasen zu veranschaulichen: Aus Karten soll ein Kartenhaus gebaut werden.

a) Wie viele Etagen kann man mit einem normalen Kartenspiel mit 32 Karten bauen?

b) Wie kommt man mit einem amerikanischen Blatt (54 Karten)?

c) Wie viel Karten benötigt man für 100 Etagen?

d) Wie viele Karten benötigt man für ein beliebig hohes Kartenhaus?

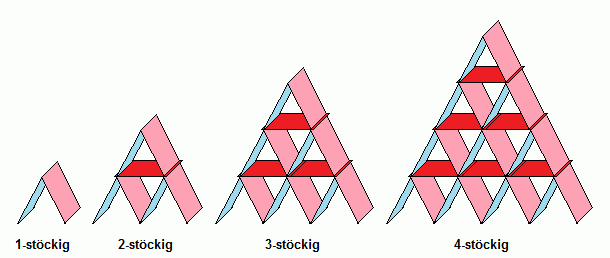
1. Die Aufgabe verstehen:
   • Bekannt ist die Anzahl der Karten oder der Etagen.
   • Gegeben ist die Anzahl der Karten (32 bzw. 54) oder die Anzahl der Etagen.
   • Die Bedingung ist das Konstruktionsprinzip: Von oben nach unten kommen in jeder Etage Karten hinzu; die unterste Etage hat keine Bodenkarten.
   • Eine Skizze hilft beim Verständnis der Struktur.
2. Einen Plan entwickeln:
   • Man kann sich einfachere Spezialfälle ansehen und die Anzahl der Karten für wenige Etagen ermitteln:
     • 1 Etage: 2 Karten
     • 2 Etagen: 7 Karten
     • 3 Etagen: 15 Karten
     • 4 Etagen: 26 Karten
   • Eine Analogie zu den Dreieckszahlen (Summe der ersten n natürlichen Zahlen: d(n)=2n(n+1)​) bietet sich an.

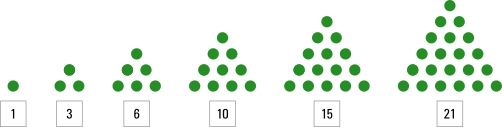
• Man kann ein Hilfselement einführen, indem man sich vorstellt, jedes Dreieck bestünde aus drei Karten, und dann die doppelt gezählten Bodenkarten abziehen.
• Die Formel für die Anzahl der Karten k(e) für e Etagen lässt sich herleiten: k(e)=3⋅d(e)−e wobei d(e) die e-te Dreieckszahl ist, also d(e)=1+2+3+…+e=2e(e+1)​. Einsetzen ergibt: k(e)=3⋅2e(e+1)​−e Vereinfacht: k(e)=23e(e+1)−2e​=23e2+3e−2e​=23e2+e​=2e(3e+1)​

3. Den Plan ausführen:
   • Für 32 Karten: k(4)=26. Mit 32 Karten sind 4 Etagen möglich, und es bleiben 6 Karten übrig.
   • Für 54 Karten: k(5)=40. k(6)=57. Mit 54 Karten sind 5 Etagen möglich, und es bleiben 14 Karten übrig.
   • Für 100 Etagen: k(100)=2100(3⋅100+1)​=15050 Karten.
4. Rückschau halten:
   • Die ersten beiden Ergebnisse können durch Zeichnung überprüft werden.
   • Eine rekursive Definition könnte ebenfalls abgeleitet werden: k(e)=k(e−1)+3e−1.
   • Die gefundene Formel und die Methode können für andere ähnliche Aufgaben nützlich sein.

Pólyas Zehn Gebote für Lehrer: Ein didaktisches Vermächtnis

Pólya hat seine Erkenntnisse auch in Zehn Geboten für Lehrer  zusammengefasst, die auch heute, fast 60 Jahre nach ihrer Formulierung, noch immer Gültigkeit besitzen und als wegweisend für den Mathematikunterricht gelten. Sie betonen die Wichtigkeit der Rolle der Lehrperson als Begleiter und Förderer:

1. Man soll sich für seinen Gegenstand interessieren.
2. Man soll seinen Gegenstand kennen.
3. Man soll über das Wesen des Lernens Bescheid wissen: Die beste Art, etwas zu erlernen, ist, es selbst zu entdecken.
4. Man soll versuchen, von den Gesichtern seiner Schüler ihre Reaktionen abzulesen, versuchen, ihre Erwartungen und Schwierigkeiten zu erkennen, sich in ihre Lage zu versetzen.
5. Man soll ihnen nicht nur Kenntnisstoff, sondern auch praktisches Können, geistige Einstellungen, methodische Arbeitsgewohnheiten vermitteln.
6. Man soll sie erraten lernen lassen.
7. Man soll sie beweisen lernen lassen.
8. Man soll auf solche Schritte bei der Lösung der Aufgabe, die man gerade durchnimmt, achten, die bei der Lösung zukünftiger Aufgaben nützlich sein könnten – man soll versuchen, das allgemeine Schema freizulegen, das der gegebenen konkreten Situation zugrunde liegt. Eine solche Diskussion fehlt oft im Unterricht.
9. Man soll nicht gleich sein ganzes Geheimnis preisgeben – man soll die Schüler raten lassen, ehe man es preisgibt – man lasse sie so viel wie irgend möglich selbst herausfinden.
10. Man lege nahe, aber man zwinge nicht auf.

Diese Prinzipien betonen die Bedeutung des aktiven Lernens, der Reflexion und der Rolle des Lehrers als kluger Begleiter, der den Lernprozess durchdacht anleitet. Pólyas Arbeiten bleiben ein unverzichtbarer Beitrag zum Verständnis und zur Förderung des Problemlösens in der Mathematik. Die Arbeit Pólyas hat enormen einfluss gehabt auf die fachdidaktische Literatur.

---