Mathematisches zum Weihnachten

Das Wichtel-Dilemma: Warum wir (fast) immer neu ziehen müssen

Es ist jedes Jahr das gleiche Spiel auf der Weihnachtsfeier: Wir schreiben Namen auf Zettel, werfen sie in einen Hut, und jeder zieht einen. Und fast immer passiert es: Ein leises Seufzen, gefolgt von einem „Halt, Stopp! Ich habe mich selbst gezogen. Alles zurück, wir müssen neu mischen!“

Man könnte meinen, das sei einfach Pech. Aber wir wissen: Zufall folgt Regeln. Und in diesem Fall ist die Mathematik ziemlich gnadenlos.

Die Intuition vs. Die Realität

Intuitiv denken wir: „Je mehr Leute mitmachen, desto unwahrscheinlicher ist es, dass ich meinen eigenen Zettel ziehe. Also müsste es in großen Gruppen seltener schiefgehen.“

Das stimmt zwar für mich als Einzelperson (meine Chance ist $1/n$ ), aber für die Gruppe als Ganzes sieht es anders aus. Die Frage ist nämlich nicht „Zieht Alex sich selbst?“, sondern „Zieht irgendjemand sich selbst?“.

Mathematisch sprechen wir hier von fixpunktfreien Permutationen (auch Derangements genannt). Wir suchen eine Anordnung der Zettel, bei der kein Element an seiner ursprünglichen Position bleibt.

Die Konstante des Scheiterns (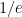 $1/e$ )

Das faszinierende an diesem Problem ist das Grenzwertverhalten. Pierre Rémond de Montmort hat dieses Problem schon im 18. Jahrhundert untersucht.

Die Wahrscheinlichkeit, dass in einer Gruppe von $n$ Personen niemand seinen eigenen Namen zieht, nähert sich mit steigendem $n$ extrem schnell einem festen Wert an:

$P(\text{Erfolg}) = \sum_{k=0}^n \frac{(-1)^k}{k!} \approx \frac{1}{e} \approx 36{,}8\,\%$

Den Beweis für diese Formal kann man sehr schön zum Beispiel mit Hilfe von dem Inklusions-Exklusions-Prinzip beweisen.

Das bedeutet im Umkehrschluss: Die Wahrscheinlichkeit, dass das Wichteln schiefgeht (mindestens einer zieht sich selbst), liegt bei:

$P(\text{Misserfolg}) \approx 1 - \frac{1}{e} \approx 63{,}2\,\%$

Das Verrückte daran ist die Stabilität dieser Zahl.

Bei 5 Personen liegt die Fehlerwahrscheinlichkeit bei ca. 63,3 %.
Bei 20 Personen liegt sie bei ca. 63,2 %.
Bei 1.000 Personen liegt sie immer noch bei ca. 63,2 %.

Es ist also fast egal, ob du mit der Familie oder einem gefüllten Fußballstadion wichtelst: In fast zwei von drei Fällen müsst ihr neu ziehen.

Überzeugen wir uns! (Monte-Carlo-Simulation)

Da wir uns gerne durch Beipiele überzeugen lassen können, lassen wir lieber den Prozessor arbeiten. Ich habe eine kleine Monte-Carlo-Simulation in Python geschrieben, um zu prüfen, ob die Theorie stimmt.

Das Skript simuliert 100.000 Wichtel-Runden für eine Gruppe von 20 Personen und zählt, wie oft es schiefgeht.

import random
import math

def wichtel_simulation(teilnehmer_anzahl, durchlaeufe=100000):
    fehlschlaege = 0
    
    for _ in range(durchlaeufe):
        # Liste von Personen erstellen [0, 1, 2, ..., n-1]
        personen = list(range(teilnehmer_anzahl))
        
        # Kopie der Liste zum Ziehen erstellen
        gezogene_lose = personen[:]
        
        # Mischen (simuliert das Ziehen)
        random.shuffle(gezogene_lose)
        
        # Pruefung: Hat jemand sich selbst gezogen?
        hat_sich_selbst_gezogen = False
        for i in range(teilnehmer_anzahl):
            if personen[i] == gezogene_lose[i]:
                hat_sich_selbst_gezogen = True
                break
        
        if hat_sich_selbst_gezogen:
            fehlschlaege += 1

    wahrscheinlichkeit = (fehlschlaege / durchlaeufe) * 100
    return wahrscheinlichkeit

if __name__ == "__main__":
    # Test mit 20 Personen
    anzahl_personen = 20
    quote = wichtel_simulation(anzahl_personen)
    
    # Theoretischer Wert (1 - 1/e)
    theorie = (1 - (1/math.e)) * 100

    print(f"Simulation mit {anzahl_personen} Personen:")
    print(f"Ergebnis: In {quote:.2f}% der Faelle zieht einer sich selbst.")
    print(f"Theoretischer Wert: ~{theorie:.2f}%")

Wenn wihr diesen Code ausführen, werden wihr sehen: Das Ergebnis pendelt sich fast immer exakt bei diesen magischen ~63,2 % ein.

Fazit: Wenn ihr das nächste Mal beim Wichteln neu ziehen müsst, ärgert euch nicht. Es ist kein Pech, es ist eine mathematische Gewissheit, präsentiert von der Eulerschen Zahl e. Alternativlösung: Nutzt einfach eine App – oder einen gerichteten Graphen (Kreiswichteln), bei dem jeder einfach dem linken Nachbarn etwas schenkt. Aber wo bleibt da der Spaß?

András Bátkai's Weblog